connected. These topologies also have interesting separation and homogeneity properties. The notion of an arithmetic progression topology can be generalized...

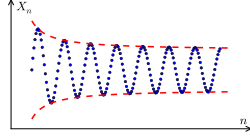
x_{\bullet }.} Arithmetic progression topologies The Baire space − N N {\displaystyle \mathbb {N} ^{\mathbb {N} }} with the product topology, where N {\displaystyle...

19th century result was Dirichlet's theorem on arithmetic progressions, that certain arithmetic progressions contain infinitely many primes. Many mathematicians...

Arithmetic progression – a sequence of numbers such that the difference between the consecutive terms is constant Generalized arithmetic progression –...

of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties...

equivalent to the divergence of the harmonic series. More generally, any arithmetic progression (i.e., a set of all integers of the form an + b with a ≥ 1, b ≥ 1...

Swiss mathematician Leonhard Euler, relies on the fundamental theorem of arithmetic: that every integer has a unique prime factorization. What Euler wrote...

equalityPages displaying short descriptions of redirect targets Arithmetic progression – Sequence of equally spaced numbers Recurrence relation – Pattern...

be expressed as a figurate number, and the formulation of the arithmetic progressions. Overbay, Shawn; Schorer, Jimmy; Conger, Heather. "Al-Khwarizmi"...

contains 33 verses covering mensuration (kṣetra vyāvahāra), arithmetic and geometric progressions, gnomon / shadows (shanku-chhAyA)[clarification needed]...

edge, the energy is the sum of an arithmetic progression, and using the formula for the sum of an arithmetic progression, one can show that E ( Z ) ≤ T (...

approximation theorem (Diophantine approximations) Dirichlet's theorem on arithmetic progressions (number theory) Dirichlet's unit theorem (algebraic number theory)...

±1-sequence Arithmetic progression Automatic sequence Cauchy sequence Constant-recursive sequence Geometric progression Harmonic progression Holonomic sequence...

.. (OEIS: A000127). Though the first five terms match the geometric progression 2n − 1, it deviates at n = 6, showing the risk of generalising from only...

Opus Geometricum (1647): "The terminus of a progression is the end of the series, which none progression can reach, even not if she is continued in infinity...

approximation theorem (diophantine approximation) Dirichlet's theorem on arithmetic progressions (number theory, specifically prime numbers) Dirichlet's unit theorem...

the primes that remain primes in Z[i]. Dirichlet's theorem on arithmetic progressions demonstrates that this is indeed the case. Even though the prime...

It uses mathematics to study elements of music such as tempo, chord progression, form, and meter. The attempt to structure and communicate new ways of...

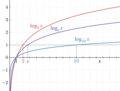
that the logarithm provides between a geometric progression in its argument and an arithmetic progression of values, prompted A. A. de Sarasa to make the...

covers the topics of definitions, arithmetical terms, interest computation, arithmetical and geometrical progressions, plane geometry, solid geometry,...

construction of large Salem–Spencer sets of integers with no three-element arithmetic progression.[B] Behrend sequences are sequences of integers whose multiples...

Infinitely Small Quantities in Leibniz's Mathematics: The Case of his Arithmetical Quadrature of Conic Sections and Related Curves". In Goldenbaum, Ursula;...

number of numbers in the collection. Arithmetic progression In mathematics, an arithmetic progression (AP) or arithmetic sequence is a sequence of numbers...

Lejeune Dirichlet proves Dirichlet's theorem about prime numbers in arithmetic progressions. 1859 — Bernhard Riemann formulates the Riemann hypothesis which...

{5}{66}}n} Indeed [if] one will have examined diligently the law of arithmetic progression there, one will also be able to continue the same without these...

Dirichlet L-functions to give the proof of Dirichlet's theorem on arithmetic progressions and began analytic number theory. In 1829, Carl Gustav Jacob Jacobi...

powers of a fundamental length, the complex dimensions appear in an arithmetic progression parallel to the imaginary axis, and are called lattice fractal strings...

on arithmetic progressions: If the sum of the reciprocals of a sequence of integers diverges, then the sequence contains arithmetic progressions of arbitrary...

shows some (rudimentary) knowledge of geometrical progression. Knowledge of arithmetic progressions is also evident from the mathematical sources. The...

to addition by making use of geometric progression of numbers and relating them to an arithmetic progression. In 1616 Henry Briggs visited John Napier...