of Betti numbers is 0 from some point onward (Betti numbers vanish above the dimension of a space), and they are all finite. The nth Betti number represents...

In persistent homology, a persistent Betti number is a multiscale analog of a Betti number that tracks the number of topological features that persist...

{otherwise}}\ ,\end{cases}}} hence has Betti number 1 in dimensions 0 and n, and all other Betti numbers are 0. Its Euler characteristic is then...

this complex is intrinsic to R, one may define the graded Betti numbers βi, j as the number of grade-j images coming from Fi (more precisely, by thinking...

studied by (Kodaira 1964, 1968) that have Kodaira dimension −∞ and first Betti number 1. Minimal surfaces of class VII (those with no rational curves with...

connection, the cyclomatic number of a graph G is also called the first Betti number of G. More generally, the first Betti number of any topological space...

{\displaystyle R_{f}} is one-dimensional, we consider only its first Betti number b 1 ( R f ) {\displaystyle b_{1}(R_{f})} ; if R f {\displaystyle R_{f}}...

n\\\{0\}&{\text{otherwise}}\end{cases}}} (see Torus § n-dimensional torus and Betti number § More examples for more details). The two independent 1-dimensional...

complexity of the program is equal to the cyclomatic number of its graph (also known as the first Betti number), which is defined as M = E − N + P . {\displaystyle...

In mathematics, L2 cohomology is a cohomology theory for smooth non-compact manifolds M with Riemannian metric. It is defined in the same way as de Rham...

persistent homology of a data set in the form of a parameterized version of a Betti number, which is called a barcode. Several branches of programming language...

others are linear combinations. In particular, this implies that the 1st Betti number of a 2-torus is two. More generally, on an n {\displaystyle n} -dimensional...

Gromov's compactness theorem (topology) in symplectic topology Gromov's Betti number theorem [ru] Gromov–Ruh theorem on almost flat manifolds Gromov's non-squeezing...

Betti may refer to: Betti (given name) Betti (surname) Betti number in topology, named for Enrico Betti Betti's theorem in engineering theory, named for...

diffeomorphic to Rn if it has positive curvature at only one point. Gromov's Betti number theorem. There is a constant C = C(n) such that if M is a compact connected...

Therefore its first Betti-number represents the doubled number of handles of the surface. With the comments above, for compact spaces all Betti-numbers are finite...

a complex, specifically the Betti number and torsion coefficients of a dimension of the complex, where the Betti number corresponds to the rank of the...

is uniquely characterized by the following properties: If the first Betti number of M is zero, λ C W L ( M ) = 1 2 | H 1 ( M ) | λ C W ( M ) {\displaystyle...

Betti number: Hopf surfaces Inoue surfaces; several other families discovered by Inoue have also been called "Inoue surfaces" Positive second Betti number:...

H 1 ( X , Z ) = 0 {\displaystyle H^{1}(X,\mathbb {Z} )=0} . Thus the Betti number b 1 ( X ) {\displaystyle b_{1}(X)} is zero, and by Poincaré duality,...

index. The Hodge diamond is In particular the first Betti number is 1 and the second Betti number is 0. Conversely Kunihiko Kodaira (1968) showed that...

Just as the number of connected components of a topological space is an important topological invariant, the zeroth Betti number, the number of components...

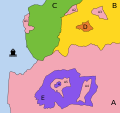
are connected surfaces. However, C and D are also simply connected surfaces, while B is not (it has first Betti number 2, the number of "holes" in B)....

Serre duality. A simple consequence of Hodge theory is that every odd Betti number b2a+1 of a compact Kähler manifold is even, by Hodge symmetry. This is...

mathematics, a Kato surface is a compact complex surface with positive first Betti number that has a global spherical shell. Kato (1978) showed that Kato surfaces...

The nonnegative integer r {\displaystyle r} is called the free rank or Betti number of the module M {\displaystyle M} . The module is determined up to isomorphism...

other i. Therefore X is a connected space, with one non-zero higher Betti number, namely, b n = 1 {\displaystyle b_{n}=1} . It does not follow that X...

Hilmar Wendt in 1934. It is the only closed flat 3-manifold with first Betti number zero. Its holonomy group is Z 2 2 {\displaystyle \mathbb {Z} _{2}^{2}}...

The smallest Listing number counts the number of connected components of a space, and is thus equivalent to the zeroth Betti number. Peirce, Charles Sanders...

that, for a closed, oriented manifold, the Betti numbers derived through simplicial homology were the same Betti numbers as those derived through de Rham...