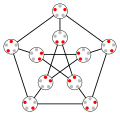
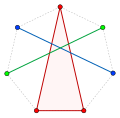
unsolved problems in mathematics The Borsuk problem in geometry, for historical reasons incorrectly called Borsuk's conjecture, is a question in discrete geometry...

In mathematics, the Bing–Borsuk conjecture states that every n {\displaystyle n} -dimensional homogeneous absolute neighborhood retract space is a topological...

In the mathematical field of geometric topology, the Poincaré conjecture (UK: /ˈpwæ̃kæreɪ/, US: /ˌpwæ̃kɑːˈreɪ/, French: [pwɛ̃kaʁe]) is a theorem about...

mathematical concepts that bear Borsuk's name include Borsuk's conjecture, Borsuk–Ulam theorem and Bing–Borsuk conjecture. In 1936, he married Zofia Paczkowska...

of graphs has a sharp phase transition, for solving Borsuk's problem (known as Borsuk's conjecture) on the number of pieces needed to partition convex...

Bing–Borsuk conjecture: every n {\displaystyle n} -dimensional homogeneous absolute neighborhood retract is a topological manifold. Borel conjecture: aspherical...

Atiyah conjecture (not a conjecture to start with) Borsuk's conjecture Chinese hypothesis (not a conjecture to start with) Doomsday conjecture Euler's...

smaller copies are needed to cover the body, as Levi already proved. Borsuk's conjecture on covering convex bodies with sets of smaller diameter Brass, Moser...

ovoidal Möbius planes. In 1993, together with Gil Kalai, he disproved Borsuk's conjecture. In 1996 he was awarded the Pólya Prize (SIAM). He was an invited...

Sylvester–Gallai theorem and De Bruijn–Erdős theorem Cauchy's theorem Borsuk's conjecture Schröder–Bernstein theorem Wetzel's problem on families of analytic...

coordinates are non-negative for points in the convex hull. Borsuk's conjecture - a conjecture about the number of pieces required to cover a body with a...

generalized Schoenflies conjecture and the double suspension theorem relied on Bing-type shrinking. Bing was fascinated by the Poincaré conjecture and made several...

number. Bing–Borsuk conjecture See Bing–Borsuk conjecture. Bockstein homomorphism Borel Borel conjecture. Borel–Moore homology Borsuk's theorem Bott 1...

cohomotopy groups, later called Borsuk–Spanier cohomotopy groups; he also founded shape theory; Borsuk's conjecture, Borsuk-Ulam theorem. Jerzy Konorski...

conjecture states that every Busemann G-space is a topological manifold. It is a special case of the Bing–Borsuk conjecture. The Busemann conjecture is...

In geometry, more specifically in polytope theory, Kalai's 3d conjecture is a conjecture on the polyhedral combinatorics of centrally symmetric polytopes...

the Petersen graph requires three colors in any proper coloring. This conjecture was proved in several ways. László Lovász proved this in 1978 using topological...

work in which she constructed a smooth counterexample to the Seifert conjecture. She has since continued to work in dynamical systems. In 1995 Kuperberg...

the book, was a proof that László Lovász published in 1978 of a 1955 conjecture by Martin Kneser, according to which the Kneser graphs K G 2 n + k , n...

applied mathematics, he proved a number of theorems and proposed several conjectures. Born into a wealthy Polish Jewish family in Lemberg, Austria-Hungary;...

Mazur–Ulam theorem Ulam's conjecture Collatz conjecture Kelly–Ulam conjecture, or reconstruction conjecture Ulam's packing conjecture Ulam matrix Ulam numbers...

Unsolved problem in mathematics Conjecture: Every bridgeless graph has a cycle-continuous mapping to the Petersen graph. More unsolved problems in mathematics...

Lovász proved the Kneser conjecture, thus beginning the new field of topological combinatorics. Lovász's proof used the Borsuk–Ulam theorem and this theorem...

Blagojević, Ziegler and Frick leads to counterexamples. Rota's basis conjecture Tverberg, H. (1966), "A generalization of Radon's theorem" (PDF), Journal...

homotopy theory Spectrum (homotopy theory) Morava K-theory Hodge conjecture Weil conjectures Directed algebraic topology Example: DE-9IM Chain complex Commutative...

graphs of the Heawood family, and it is conjectured that this list is complete. Colin de Verdière (1990) conjectured that any graph with Colin de Verdière...

conservation law. 1916 – Srinivasa Ramanujan introduces Ramanujan conjecture. This conjecture is later generalized by Hans Petersson. 1919 – Viggo Brun defines...

Lovász proved the Kneser conjecture, thus beginning the new study of topological combinatorics. Lovász's proof used the Borsuk-Ulam theorem and this theorem...

Thomas Callister Hales proves the Kepler conjecture, 2003 – Grigori Perelman proves the Poincaré conjecture, 2007 – a team of researchers throughout North...

condition for the FPP to hold. The problem was open for 20 years until the conjecture was disproved by Kinoshita who found an example of a compact contractible...