In abstract algebra, a normal subgroup (also known as an invariant subgroup or self-conjugate subgroup) is a subgroup that is invariant under conjugation...
19 KB (3,156 words) - 00:46, 23 May 2025
about c-normal subgroups: Every normal subgroup is c-normal Every retract is c-normal Every c-normal subgroup is weakly c-normal Y. Wang, c-normality...
895 bytes (126 words) - 22:11, 1 October 2023
group theory, the Fitting subgroup F of a finite group G, named after Hans Fitting, is the unique largest normal nilpotent subgroup of G. Intuitively, it...
9 KB (1,318 words) - 01:46, 6 September 2022
Core (group theory) (redirect from Core-free subgroup)
special normal subgroups of a group. The two most common types are the normal core of a subgroup and the p-core of a group. For a group G, the normal core...
8 KB (1,171 words) - 21:48, 24 April 2025
Centralizer and normalizer (redirect from C closed subgroup)
confused with the normal closure. Clearly C G ( S ) ⊆ N G ( S ) {\displaystyle C_{G}(S)\subseteq N_{G}(S)} and both are subgroups of G {\displaystyle...
15 KB (2,241 words) - 07:28, 25 May 2025
important because it is the smallest normal subgroup such that the quotient group of the original group by this subgroup is abelian. In other words, G / N...
11 KB (1,833 words) - 17:10, 24 April 2023
monomorphism f from H to G is normal if and only if its image is a normal subgroup of G. In particular, if H is a subgroup of G, then the inclusion map...
2 KB (280 words) - 00:37, 11 January 2025
{n}},\quad b,c\equiv 0{\pmod {n}}\right\}} This definition immediately implies that Γ ( n ) {\displaystyle \Gamma (n)} is a normal subgroup of finite index...
27 KB (4,782 words) - 22:03, 27 March 2025
element is always a normal subgroup of the original group, and the other equivalence classes are precisely the cosets of that normal subgroup. The resulting...
20 KB (3,753 words) - 13:10, 26 June 2025
{\displaystyle gHg^{-1}} of a subgroup H in G is equal to the index of the normalizer of H in G. If H is a subgroup of G, the index of the normal core of H satisfies...
16 KB (2,612 words) - 00:37, 6 December 2024
Solvable group (redirect from Solvable subgroup)
of the cyclic groups. Z 4 {\displaystyle \mathbb {Z} _{4}} is not a normal subgroup. A group G is called solvable if it has a subnormal series whose factor...
18 KB (3,033 words) - 00:00, 23 April 2025
Sylow theorems (redirect from Sylow subgroup)
p} . A Sylow p-subgroup (sometimes p-Sylow subgroup) of a finite group G {\displaystyle G} is a maximal p {\displaystyle p} -subgroup of G {\displaystyle...
33 KB (4,453 words) - 21:57, 24 June 2025
In group theory, the normal closure of a subset S {\displaystyle S} of a group G {\displaystyle G} is the smallest normal subgroup of G {\displaystyle...
4 KB (606 words) - 23:27, 1 April 2025
Coset (section Normal subgroups)
elements of every subgroup H of G divides the number of elements of G. Cosets of a particular type of subgroup (a normal subgroup) can be used as the...
28 KB (3,443 words) - 04:43, 23 January 2025
A, B, and C subgroups of a group with A ≤ C (A a subgroup of C) then AB ∩ C = A(B ∩ C); the multiplication here is the product of subgroups. This property...
10 KB (1,120 words) - 09:32, 8 July 2025
Symmetric group (redirect from Transitive subgroup)
form a subgroup of index 2 in S, called the alternating subgroup A. Since A is even a characteristic subgroup of S, it is also a normal subgroup of the...
46 KB (6,212 words) - 00:59, 12 July 2025
Direct product of groups (section Subgroups)
product of its subgroups G and H. In some contexts, the third property above is replaced by the following: 3′. Both G and H are normal in P. This property...
26 KB (2,932 words) - 23:03, 19 April 2024
Isomorphism theorems (section Theorem C (groups))
_{2}(\mathbb {C} )} , the subgroup of determinant 1 matrices, and N {\displaystyle N} the normal subgroup of scalar matrices C × I = { ( a 0 0 a ) : a ∈ C × } {\displaystyle...
25 KB (3,607 words) - 19:19, 19 July 2025
}(G)} to denote the number of maximal and normal subgroups of index n {\displaystyle n} , respectively. Subgroup growth studies these functions, their interplay...
8 KB (1,641 words) - 23:49, 27 June 2023
H {\displaystyle f:G\rightarrow H} , let N {\displaystyle N} be a normal subgroup in G {\displaystyle G} and φ {\displaystyle \varphi } the natural surjective...
8 KB (1,377 words) - 11:55, 15 June 2025
a subgroup H, and a normal subgroup N ◃ G {\displaystyle N\triangleleft G} , the following statements are equivalent: G is the product of subgroups, G...
30 KB (4,551 words) - 17:09, 25 July 2025
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple...
16 KB (2,136 words) - 01:30, 1 July 2025
Discrete group (redirect from Discrete subgroup)
Discrete normal subgroups play an important role in the theory of covering groups and locally isomorphic groups. A discrete normal subgroup of a connected...
7 KB (899 words) - 11:34, 23 October 2024
group G: G has a central series of finite length. That is, a series of normal subgroups { 1 } = G 0 ◃ G 1 ◃ ⋯ ◃ G n = G {\displaystyle \{1\}=G_{0}\triangleleft...
15 KB (1,912 words) - 08:01, 24 April 2025
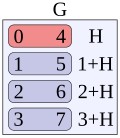
Dihedral group of order 8 (section Normal subgroups)
of these normal subgroups, shown with a red background. In this table r means rotations, and f means flips. Because this subgroup is normal, the left...
15 KB (1,028 words) - 06:05, 21 July 2025
describes the relation between representations of a group and those of a normal subgroup. Alfred H. Clifford proved the following result on the restriction...
6 KB (1,015 words) - 21:19, 6 June 2025
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
7 KB (924 words) - 00:02, 6 December 2024
Algebraic group (redirect from Algebraic subgroup)
subgroup is said to be normal if it is stable under every inner automorphism (which are regular maps). If H {\displaystyle \mathrm {H} } is a normal algebraic...
16 KB (2,244 words) - 15:28, 15 May 2025
mathematical field of group theory, Lagrange's theorem states that if H is a subgroup of any finite group G, then | H | {\displaystyle |H|} is a divisor of |...
17 KB (2,250 words) - 08:10, 23 July 2025
Lie group (redirect from Lie subgroup)
connected normal solvable subgroup Gnil for the largest connected normal nilpotent subgroup so that we have a sequence of normal subgroups 1 ⊆ Gnil ⊆...
65 KB (9,490 words) - 15:29, 22 April 2025