In set theory, Cantor's paradox states that there is no set of all cardinalities. This is derived from the theorem that there is no greatest cardinal number...

numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of. Originally, Cantor's theory of transfinite numbers...

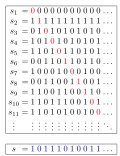
Cantor's diagonal argument (among various similar names) is a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence...

{N} } , proving Cantor's theorem. Cantor's theorem and its proof are closely related to two paradoxes of set theory. Cantor's paradox is the name given...

universal set, so it must be that Cantor's theorem (in its original form) does not hold in NF. Indeed, the proof of Cantor's theorem uses the diagonalization...

theory, for instance Cantor's paradox and the Burali-Forti paradox, and did not believe that they discredited his theory. Cantor's paradox can actually be...

negation The smallest uninteresting integer paradox Girard's paradox in type theory Basic Law V Cantor's diagonal argument – Proof in set theory Gödel's...

After the discovery of paradoxes within naive set theory (such as Russell's paradox, Cantor's paradox and the Burali-Forti paradox), various axiomatic systems...

Burali-Forti paradox: If the ordinal numbers formed a set, it would be an ordinal number that is smaller than itself. Cantor's paradox: The set of all...

{\displaystyle \bot } Cantor's theorem Gödel's incompleteness theorems Halting problem List of paradoxes Self-reference List of self–referential paradoxes Double bind...

Zeno's paradoxes are a series of philosophical arguments presented by the ancient Greek philosopher Zeno of Elea (c. 490–430 BC), primarily known through...

algebraic numbers, and gave feedback and modifications on Cantor's proofs before publishing. After Cantor's 1883 proof that all finite-dimensional spaces ( R...

the "hypergame paradox" a self-referential, set-theoretic paradox like Russell's paradox and Cantor's paradox. The hypergame paradox arises from trying...

ZFC is immune to the classic paradoxes of naive set theory: Russell's paradox, the Burali-Forti paradox, and Cantor's paradox. Abian & LaMacchia (1978) studied...

absolute infinite in Cantor's conception of set". Erkenntnis. 42 (3): 375–402. doi:10.1007/BF01129011. JSTOR 20012628. S2CID 122487235. Cantor (1) took the absolute...

Burali-Forti paradox Cantor's back-and-forth method Cantor's diagonal argument Cantor's first uncountability proof Cantor's paradox Cantor's theorem Cantor–Bernstein–Schroeder...

The Banach–Tarski paradox is a theorem in set-theoretic geometry that states the following: Given a solid ball in three-dimensional space, there exists...

those of finite collections of things. The paradox of Hilbert's Grand Hotel can be understood by using Cantor's theory of transfinite numbers. Thus, in an...

most countable model. However, Cantor's theorem proves that there are uncountable sets. The root of this seeming paradox is that the countability or noncountability...

poset paradox 1.  Berry's paradox 2.  Burali-Forti's paradox 3.  Cantor's paradox 4.  Hilbert's paradox 5.  König's paradox 6.  Milner–Rado paradox 7.  Richard's...

1874, Cantor proved that the real numbers were uncountable; in 1891, he proved by his diagonal argument the more general result known as Cantor's theorem:...

Burali-Forti paradox. Georg Cantor had apparently discovered the same paradox in his (Cantor's) "naive" set theory and this become known as Cantor's paradox. Russell's...

Cantor's first set theory article contains Georg Cantor's first theorems of transfinite set theory, which studies infinite sets and their properties....

paradox) in this treatment (Cantor's paradox), by Russell's discovery (1902) of an antinomy in Frege's 1879 (Russell's paradox), by the discovery of more...

arguments in mathematics and logic, such as Cantor's diagonal argument, Cantor's theorem, Russell's paradox, Gödel's first incompleteness theorem, Turing's...

Philip Jourdain and/or Georg Cantor to avoid Cantor's paradox. It identifies certain "inconsistent multiplicities", in Cantor's terminology, that cannot be...

theorem Cantor's first set theory article Cantor's leaky tent Cantor's paradox Cantor's theorem Cantor–Bendixson rank Cantor–Bendixson theorem Cantor–Bernstein...

set of all sets, provided that both exist. However, this conflicts with Cantor's theorem that the power set of any set (whether infinite or not) always...

the proofs of the following theorems: Cantor's diagonal argument (the earliest) Cantor's theorem Russell's paradox Diagonal lemma Gödel's first incompleteness...

set; a vital part of Zermelo–Fraenkel set theory. Moreover, in 1899, Cantor's paradox was discovered. It postulates that there is no set of all cardinalities...