In vector calculus, a conservative vector field is a vector field that is the gradient of some function. A conservative vector field has the property...

vector calculus a solenoidal vector field (also known as an incompressible vector field, a divergence-free vector field, or a transverse vector field)...

force field F, defined everywhere in space (or within a simply-connected volume of space), is called a conservative force or conservative vector field if...

In vector calculus and physics, a vector field is an assignment of a vector to each point in a space, most commonly Euclidean space R n {\displaystyle...

force field is a vector field corresponding with a non-contact force acting on a particle at various positions in space. Specifically, a force field is a...

codomain, Conservative vector field, a vector field that is the gradient of a scalar potential field Hamiltonian vector field, a vector field defined for...

In vector calculus, the gradient of a scalar-valued differentiable function f {\displaystyle f} of several variables is the vector field (or vector-valued...

In vector calculus, a complex lamellar vector field is a vector field which is orthogonal to a family of surfaces. In the broader context of differential...

Vector calculus or vector analysis is a branch of mathematics concerned with the differentiation and integration of vector fields, primarily in three-dimensional...

called conservative forces. If the force acting on a body varies over space, then one has a force field; such a field is described by vectors at every...

a vector flow can be thought of as a solution to the system of differential equations induced by a vector field. That is, if a (conservative) vector field...

justification for belief Conservative force, a physical force whose work is path-independent Conservative vector field, a vector field that is the gradient...

In vector calculus, a Beltrami vector field, named after Eugenio Beltrami, is a vector field in three dimensions that is parallel to its own curl. That...

curve (commonly arc length or, for a vector field, the scalar product of the vector field with a differential vector in the curve). This weighting distinguishes...

field line is a graphical visual aid for visualizing vector fields. It consists of an imaginary integral curve which is tangent to the field vector at...

{\displaystyle \phi } is a scalar potential for the irrotational/conservative vector field E → {\displaystyle {\vec {E}}} ) and A → ( x → , t ) {\displaystyle...

exact form. In 3 dimensions, an exact vector field (thought of as a 1-form) is called a conservative vector field, meaning that it is the derivative (gradient)...

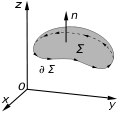
in vector calculus on R 3 {\displaystyle \mathbb {R} ^{3}} . Given a vector field, the theorem relates the integral of the curl of the vector field over...

that V is a scalar potential of the conservative vector field F. Scalar potential is not determined by the vector field alone: indeed, the gradient of a...

if the vector field F is the gradient of some scalar-valued function (i.e., if F is conservative), then F is a path-independent vector field (i.e., the...

any C 1 {\displaystyle C^{1}} vector field that has the path-independence property (so it is a conservative vector field.) must also be irrotational and...

electric field between atoms is the force responsible for chemical bonding that result in molecules. The electric field is defined as a vector field that...

of which is characterized by an irrotational solenoidal field or a conservative vector field. Control System Analysis: Control Systems - The application...

conservative vector field this integral evaluates to zero for every closed curve. That means that a line integral between any two points in the field...

its reciprocal density (ρ) Particle number (ni) Markov property Conservative vector field Nonholonomic system Equation of state State variable Callen 1985...

point can be used. In classical electrostatics, the electrostatic field is a vector quantity expressed as the gradient of the electrostatic potential...

In science, a field is a physical quantity, represented by a scalar, vector, or tensor, that has a value for each point in space and time. An example...

curl, denoted ∇×, of the vector field vanishes. In the case of the gravitational field g, which can be shown to be conservative, it is equal to the gradient...

vector.: 93  Not all central force fields are conservative or spherically symmetric. However, a central force is conservative if and only if it is spherically...

solving non-exact differential equations by making them exact Conservative vector field Laidler, Keith, J. (1993). The World of Physical Chemistry. Oxford...