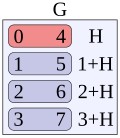
In mathematics, coset enumeration is the problem of counting the cosets of a subgroup H of a group G given in terms of a presentation. As a by-product...

set of G into disjoint, equal-size subsets called cosets. There are left cosets and right cosets. Cosets (both left and right) have the same number of elements...

coset enumeration problem. Given a presentation of a group G by generators and relations and a subgroup H of G, the algorithm enumerates the cosets of...

Italian school of algebraic geometry. The Todd–Coxeter process for coset enumeration is a major method of computational algebra, and dates from a collaboration...

graph of (G, S). The graph is useful to understand coset enumeration and the Todd–Coxeter algorithm. Coset graphs can be used to form large permutation representations...

permutation group the Todd–Coxeter algorithm and Knuth–Bendix algorithm for coset enumeration the product-replacement algorithm for finding random elements of a...

{\displaystyle \Gamma } is disconnected and each connected component represents a coset of the subgroup generated by S {\displaystyle S} . If an element s {\displaystyle...

work with because they are ill-suited to standard methods such as coset enumeration. In topology, groups can often be described as finitely presented...

∈ G } {\displaystyle G\cdot x=\{g\cdot x:g\in G\}} and the set of left cosets G / G x {\displaystyle G/G_{x}} . Lagrange's theorem implies that | G ⋅...

concerns the enumeration of combinatorial structures using tools from complex analysis and probability theory. In contrast with enumerative combinatorics...

moonshine Projective representation Representation theory Schur's lemma Coset enumeration Schreier's subgroup lemma Schreier–Sims algorithm Todd–Coxeter algorithm...

repeated, generating the whole coset S k − 1 τ 1 {\displaystyle S_{k-1}\tau _{1}} , reaching the last permutation in that coset λ k − 1 τ 1 {\displaystyle...

n {\displaystyle n} . Then G {\displaystyle G} acts on the set of left cosets of U {\displaystyle U} in G {\displaystyle G} by left shift: g ( h U ) =...

from each right (respectively left) coset of H. In this case, the "sets" (cosets) are mutually disjoint, i.e. the cosets form a partition of the group. As...

whose index is 2. Elements of the coset 0 + I {\displaystyle 0+I} may be called even, while elements of the coset 1 + I {\displaystyle 1+I} may be called...

are in GenP for all fixed finitely presented groups. The well known coset enumeration procedure admits a computable upper bound on a generic set of inputs...

polyhedron, the polyhedra can be identified with the orbit space G/H – the coset gH corresponds to which polyhedron g sends the chosen polyhedron to. There...

{R} /\mathbb {Q} } of these two groups which is the group formed by the cosets r + Q {\displaystyle r+\mathbb {Q} } of the rational numbers as a subgroup...

uncountability of the real numbers Combinatorics Combinatory logic Co-NP Coset Countable countability of a subset of a countable set (to do) Angle of parallelism...

These were enumerated by length in (Hanusa & Jones 2010). The parabolic subgroups of S ~ n {\displaystyle {\widetilde {S}}_{n}} and their coset representatives...

"The Converse of the Intermediate Value Theorem: From Conway to Cantor to Cosets and Beyond" Missouri J. Math. Sci. 26 (2): 134–150 "Large Numbers, Part...

G {\displaystyle e:J\to G} . Instead an enumeration of homomorphisms is used, and since such an enumeration can be constructed uniformly, it results...

original Coxeter polytope in a manner prescribed by an appropriate Schreier coset graph). In the previous construction the manifolds obtained are always compact...

left) Each row is a coset with the coset leader in the first column The entry in the i-th row and j-th column is the sum of the i-th coset leader and the j-th...

( V ) / H {\displaystyle \mathbf {Gr} (k,V)=\mathrm {GL} (V)/H} of left cosets of H {\displaystyle H} . If the underlying field is R {\displaystyle \mathbf...

elements of the Klein four-group. As with any connected Lie group, the coset spaces of the closed subgroups of the restricted Lorentz group, or homogeneous...

size n. Then the pure state space of Hn can be identified with the compact coset space U ⁡ ( n ) / ( U ⁡ ( n − 1 ) × U ⁡ ( 1 ) ) . {\displaystyle \operatorname...

with subscript i 0 {\displaystyle i_{0}} which represents the principal coset (i.e., the subgroup H {\displaystyle H} itself) may be, but need not be...

p. 17 Jones, Andrew R. (1996), "A Combinatorial Approach to the Double Cosets of the Symmetric Group with respect to Young Subgroups", European Journal...

modeled on the decomposition of the real coordinate space Rn into the cosets x + Rp of the standardly embedded subspace Rp. The equivalence classes are...