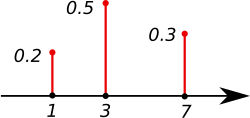
In mathematics, specifically measure theory, the counting measure is an intuitive way to put a measure on any set – the "size" of a subset is taken to...

{\displaystyle \mathbb {C} } ) its Haar measure is the angle measure. For a discrete group the counting measure is a Haar measure. Every (pseudo) Riemannian manifold...

the Dirac measure and X n {\displaystyle X_{n}} are random variables, is called a point process or random counting measure. This random measure describes...

the stationary measure is the counting measure, the measure μ P {\displaystyle \mu _{P}} is the product of counting measures. The Markov chain is ergodic...

{\displaystyle S} is { 1 , … , n } {\displaystyle \{1,\dots ,n\}} with the counting measure, we have ∑ k = 1 n | x k y k | ≤ ( ∑ k = 1 n | x k | p ) 1 p ( ∑ k...

players. Counting measure – Mathematical concept Approximate number system – Innate ability to detect differences in magnitude without counting Gleadow...

the counting measure, if it exists, is the Radon–Nikodym derivative of the pushforward measure of X {\displaystyle X} (with respect to the counting measure)...

In Japanese, counter words or counters are measure words used with numbers to count things, actions, and events. Counters are added directly after numbers...

are not examples of Radon measures: Counting measure on Euclidean space is an example of a measure that is not a Radon measure, since it is not locally...

counting measure; the measure of any finite set is the number of elements in the set, and the measure of any infinite set is infinity. This measure is...

to each element. Counting sometimes involves numbers other than one; for example, when counting money, counting out change, "counting by twos" (2, 4, 6...

Lebesgue measure. Look at some measurable space ( X , A ) {\displaystyle (X,{\mathcal {A}})} and let μ {\displaystyle \mu } be the counting measure, so μ...

it carries an essentially unique natural measure, the Haar measure, which allows one to consistently measure the "size" of sufficiently regular subsets...

measure. On compact (or σ-compact) metric spaces, Borel sets are the same as Baire sets and Borel measures are the same as Baire measures. Counting measure...

Lebesgue measure Lebesgue integration Lebesgue's density theorem Counting measure Complete measure Haar measure Outer measure Borel regular measure Radon...

Brown measure of an operator in a finite factor is a probability measure on the complex plane which may be viewed as an analog of the spectral counting measure...

process can be considered as a counting measure, so points processes are types of random measures known as random counting measures. In this context, the Poisson...

numbers may be termed count chant, "to identify it as a unique instructional process." In lieu of simply counting the beats of a measure, other systems can...

decomposable into measures on continua, and a finite or countable counting measure. Inner measure Lebesgue measurable set – Concept of area in any dimensionPages...

reference measure is the Lebesgue measure. The probability mass function of a discrete random variable is the density with respect to the counting measure over...

measures that occur in practice are σ-finite. Counting measure on an uncountable measure space with all subsets measurable is a decomposable measure that...

omer still has a purpose as a remembrance of the counting up to Sinai. One explanation for the Counting of the Omer is that it shows the connection between...

the unit interval with Lebesgue measure and Y {\displaystyle Y} is the unit interval with the discrete counting measure. Let the ring R {\displaystyle...

and a (left and right invariant) Haar measure on G {\displaystyle G} is the counting measure. The Haar measure on the topological group ( R , + ) {\displaystyle...

lines of code (LOC), is a software metric used to measure the size of a computer program by counting the number of lines in the text of the program's source...

Radon measure is locally finite. The counting measure is sometimes locally finite and sometimes not: the counting measure on the integers with their usual...

respect to this dominating measure. Discrete densities are usually defined as this derivative with respect to a counting measure over the set of all possible...

set. Thus, the concept of the Hausdorff measure generalizes the Lebesgue measure and its notions of counting, length, and area. It also generalizes volume...

issue often called 'double counting', wherein the total value of a good is included several times in national output, by counting it repeatedly in several...

{P}}(\mathbb {R} ),\nu )} where ν {\displaystyle \nu } denotes the counting measure. This space is atomic, with all atoms being the singletons, yet the...