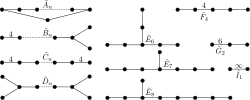
In mathematics, a Coxeter element is an element of an irreducible Coxeter group which is a product of all simple reflections. The product depends on the...

In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic...

the Coxeter graph, Coxeter groups, Coxeter's loxodromic sequence of tangent circles, Coxeter–Dynkin diagrams, and the Todd–Coxeter algorithm. Coxeter was...

In mathematics, the longest element of a Coxeter group is the unique element of maximal length in a finite Coxeter group with respect to the chosen generating...

identity element of W) and W S = W {\displaystyle W_{S}=W} . The pair ( W I , I ) {\displaystyle (W_{I},I)} is again a Coxeter group. Moreover, the Coxeter group...

a Coxeter–Dynkin diagram (or Coxeter diagram, Coxeter graph) is a graph with numerically labeled edges (called branches) representing a Coxeter group...

the four-dimensional measure polytope, taken as a unit for hypervolume. Coxeter labels it the γ4 polytope. The term hypercube without a dimension reference...

generated by some subset of S). A Coxeter matroid is a subset M of W/P that for every w in W, M contains a unique minimal element with respect to the w-Bruhat...

Coxeter element s 0 ⋅ s 1 ⋯ s n − 1 {\displaystyle s_{0}\cdot s_{1}\cdots s_{n-1}} in S ~ n {\displaystyle {\widetilde {S}}_{n}} is a Coxeter element...

two reduced words of a Coxeter group to represent the same element. If two reduced words represent the same element of a Coxeter group, then Matsumoto's...

=e_{1}e_{2}\cdots e_{n}.} This is both a Coxeter element of sorts (product of reflections) and a longest element of a Coxeter group in the Bruhat order; this is...

or 5-orthoplex. Coxeter, Regular Polytopes, sec 1.8 Configurations Coxeter, Complex Regular Polytopes, p.117 H.S.M. Coxeter: Coxeter, Regular Polytopes...

In group theory, the Todd–Coxeter algorithm, created by J. A. Todd and H. S. M. Coxeter in 1936, is an algorithm for solving the coset enumeration problem...

corresponds to the identity element of the Weyl group, and the dual top-dimensional cell corresponds to the longest element of a Coxeter group. There are a number...

pentachoron, pentatope, pentahedroid, tetrahedral pyramid, or 4-simplex (Coxeter's α 4 {\displaystyle \alpha _{4}} polytope), the simplest possible convex...

mathematics, the Coxeter complex, named after H. S. M. Coxeter, is a geometrical structure (a simplicial complex) associated to a Coxeter group. Coxeter complexes...

Hecke and Nagayoshi Iwahori, is a deformation of the group algebra of a Coxeter group. Hecke algebras are quotients of the group rings of Artin braid groups...

n Coxeter group has n mirrors and is represented by a Coxeter–Dynkin diagram. Coxeter notation offers a bracketed notation equivalent to the Coxeter diagram...

Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter...

alternately labeled (checkerboarded) facets, with Schläfli symbol {3,3,31,1} or Coxeter symbol 211. It is a part of an infinite family of polytopes, called cross-polytopes...

hyperbolic Coxeter groups, or 4-prisms, of rank 5, each generating uniform honeycombs in hyperbolic 4-space as permutations of rings of the Coxeter diagrams...

Coxeter 1973, § 1.8 Configurations Coxeter, Complex Regular Polytopes, p.117 Conway, Burgiel & Goodman-Strauss 2008, p. 406, Fig 26.2 Coxeter, Star...

The Goldberg–Coxeter construction or Goldberg–Coxeter operation (GC construction or GC operation) is a graph operation defined on regular polyhedral graphs...

unoriented diagram (a special kind of Coxeter diagram), the Weyl group (a concrete reflection group), or the abstract Coxeter group. Although the Weyl group...

as HM5 for a 5-dimensional half measure polytope. Coxeter named this polytope as 121 from its Coxeter diagram, which has branches of length 2, 1 and 1...

BσB is determined by the length of σ as an element of W. The dimension is maximized at the Coxeter element and gives the unique open dense double coset...

Honeycombs under advisor Coxeter, completes the basic theory of uniform polytopes for dimensions 4 and higher. 1986 Coxeter published a paper Regular...

symmetry can be generated by these three Coxeter groups, represented by permutations of rings of the Coxeter-Dynkin diagrams: Selected regular and uniform...

as HM7 for a 7-dimensional half measure polytope. Coxeter named this polytope as 141 from its Coxeter diagram, with a ring on one of the 1-length branches...

1983 Bertram Kostant (Massachusetts Institute of Technology): On the Coxeter element and the structure of the exceptional Lie groups. 1984 Barry Mazur (Harvard...