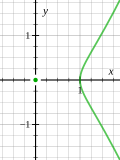
such a singularity is in the same differential class as the cusp of equation x 2 − y 5 = 0 , {\displaystyle x^{2}-y^{5}=0,} which is a singularity of type...

In mathematics, a cusp neighborhood is defined as a set of points near a cusp singularity. The cusp neighborhood for a hyperbolic Riemann surface can...

coordinate system has a singularity (called a cusp) at ( 0 , 0 ) {\displaystyle (0,0)} . For singularities in algebraic geometry, see singular point of an algebraic...

a pointed structure on a tooth. Cusp or CUSP may also refer to: Cusp (singularity), a singular point of a curve Cusp catastrophe, a branch of bifurcation...

mathematical singularity as a value at which a function is not defined. For that, see for example isolated singularity, essential singularity, removable...

dynamical systems; it is also a particular special case of more general singularity theory in geometry. Bifurcation theory studies and classifies phenomena...

C={\text{Spec}}\left({\frac {k[x,y]}{y^{2}-x^{5}}}\right)} with the cusp singularity at the origin. Its normalization can be given by the map Spec ( k [...

singular point at the origin. However, a node such as that of y 2 − x 3 − x 2 = 0 {\displaystyle y^{2}-x^{3}-x^{2}=0} at the origin is a singularity of...

astroid is a particular type of roulette curve: a hypocycloid with four cusps. Specifically, it is the locus of a point on a circle as it rolls inside...

as patches of light or their bright edges, shapes which often have cusp singularities. Concentration of light, especially sunlight, can burn. The word caustic...

Noetherian domain that is not a J-1 ring as S has a cusp singularity at every closed point, so the set of singular points is not closed, though it is a G-ring...

link of the cusp singularity z 2 + w 3 {\displaystyle z^{2}+w^{3}} ; the Hopf link (oriented correctly) is the link of the node singularity z 2 + w 2 {\displaystyle...

measurements of the expansion rate of the universe place the Big Bang singularity at an estimated 13.787±0.02 billion years ago, which is considered the...

In mathematics, the signature defect of a singularity measures the correction that a singularity contributes to the signature theorem. Hirzebruch (1973)...

cusps. This curve was further studied by Arthur Cayley in 1867. The bicorn is a plane algebraic curve of degree four and genus zero. It has two cusp singularities...

corresponding to the cusps of the action. It is compact, and has not only the quotient singularities of X, but also singularities at its cusps. The surface Y...

the rhamphoid cusp y2 = x5 has a singularity of order 2 at the origin. After blowing up at its singular point it becomes the ordinary cusp y2 = x3, which...

geometry, a tacnode (also called a point of osculation or double cusp) is a kind of singular point of a curve. It is defined as a point where two (or more)...

S} -module. Also S {\displaystyle S} has a cusp singularity at every closed point, so the set of singular points is not closed. (Danilov 2001) Akizuki...

must have a local minimum or a local maximum at the singularity. Singular point of a curve Crunode Cusp Tacnode Hazewinkel, M. (2001) [1994], "Acnode", Encyclopedia...

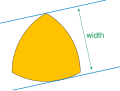
of constant width from involutes of curves with an odd number of cusp singularities, having only one tangent line in each direction (that is, projective...

is not a J-0 ring. More precisely S has a cusp singularity at every closed point, so the set of non-singular points consists of just the ideal (0) and...

equations of the branches. For describing a singularity, it is worth to translate the curve for having the singularity at the origin. This consists of a change...

Cuspidal point can refer to: Cuspidal point of a curve, see Cusp (singularity) Cuspidal point of a surface, see Pinch point (mathematics) This disambiguation...

generally called jets. The point of osculation is also called the double cusp. Contact is a geometric notion; it can be defined algebraically as a valuation...

points converge to the singular point and only 3 inflection remain along the singular curve. If the cubic degenerates and gets a cusp then only one inflection...

a curve will generically have a cusp when the curve has a vertex; other, more degenerate and non-stable singularities may occur at higher-order vertices...

transition of a soap film surface by the emergence of a twisted fold (cusp) singularity. His current work aims to establish connections between isophase minimal...

and at all cusps of G. Again, modular forms that vanish at all cusps are called cusp forms for G. The C-vector spaces of modular and cusp forms of weight...

by James Gregory in letters to Collins (1670–1671), ibid. This singularity is a cusp of the second kind, in which both branches are concave from the...