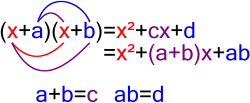In mathematics, the Dickson polynomials, denoted Dn(x,α), form a polynomial sequence introduced by L. E. Dickson (1897). They were rediscovered by Brewer...

case the ring is a finite field, the Dickson polynomials, which are closely related to the Chebyshev polynomials, provide examples. Over a finite field...

Brahmagupta polynomials Caloric polynomial Charlier polynomials Chebyshev polynomials Chihara–Ismail polynomials Cyclotomic polynomials Dickson polynomial Ehrhart...

The Chebyshev polynomials are two sequences of orthogonal polynomials related to the cosine and sine functions, notated as T n ( x ) {\displaystyle T_{n}(x)}...

All-one polynomials Abel polynomials Bell polynomials Bernoulli polynomials Cyclotomic polynomials Dickson polynomials Fibonacci polynomials Lagrange...

Leonard Eugene Dickson (January 22, 1874 – January 17, 1954) was an American mathematician. He was one of the first American researchers in abstract algebra...

{\displaystyle x^{2}+x+41} are all prime. When all the polynomials have degree 1, this is the original Dickson's conjecture. This generalization is equivalent...

example, 3 × 5 is an integer factorization of 15, and (x − 2)(x + 2) is a polynomial factorization of x2 − 4. Factorization is not usually considered meaningful...

polynomials, other expressions, or values in systems of mathematical values other than the numbers. For instance, the square of the linear polynomial...

octonion algebra. The variables must be non-commutative otherwise the second polynomial would be identically zero. Adding a representation of the 14 generators...

_{x{\bmod {p}}}{\binom {D_{n+1}(x,a)}{p}}} where Dn is the Dickson polynomial (or "Brewer polynomial") given by D 0 ( x , a ) = 2 , D 1 ( x , a ) = x , D n...

study of algebraic equations (also called "polynomial equations"), which are equations defined by a polynomial. The main problem of the theory of equations...

produce zero. The algorithm terminates always because of Dickson's lemma or because polynomial rings are Noetherian (Hilbert's basis theorem). Condition...

"Galois field". In a finite field of order q {\displaystyle q} , the polynomial X q − X {\displaystyle X^{q}-X} has all q {\displaystyle q} elements of...

In mathematics, a Diophantine equation is an equation, typically a polynomial equation in two or more unknowns with integer coefficients, for which only...

called Dickson invariants. Dickson proved that the full ring of invariants Fq[X1, ...,Xn]GLn(Fq) is a polynomial algebra over the n Dickson invariants...

polynomials, Buchberger's algorithm is a method for transforming a given set of polynomials into a Gröbner basis, which is another set of polynomials...

bicomplex number is a pair (w, z) of complex numbers constructed by the Cayley–Dickson process that defines the bicomplex conjugate ( w , z ) ∗ = ( w , − z )...

for a permutation group G is a polynomial whose coefficients depend polynomially on the coefficients of a given polynomial p and has, roughly speaking,...

Under this correspondence, Dickson's lemma may be seen as a special case of Hilbert's basis theorem stating that every polynomial ideal has a finite basis...

Bunyakovsky conjecture (or Bouniakowsky conjecture) gives a criterion for a polynomial f ( x ) {\displaystyle f(x)} in one variable with integer coefficients...

defined with respect to polynomials of degree at least 2, but they have been most extensively studied in the case of quadratic polynomials. The definition of...

wider set of algebraic numbers (all solutions to polynomial equations). Galois (1832) linked polynomial equations to group theory giving rise to the field...

RSA-inspired cryptographic accumulator. Naccache also noted that the Dickson polynomials are quasi-commutative in the degree, but it is unknown whether this...

description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely...

In number theory, the Chevalley–Warning theorem implies that certain polynomial equations in sufficiently many variables over a finite field have solutions...

In mathematics, Sophie Germain's identity is a polynomial factorization named after Sophie Germain stating that x 4 + 4 y 4 = ( ( x + y ) 2 + y 2 ) ⋅ (...

Another proof was given by Leonard Eugene Dickson shortly after Wedderburn's original proof, and Dickson acknowledged Wedderburn's priority. However...

and its characteristic- and minimal polynomials. For any z in C define the following real quadratic polynomial: Q ( z ; x ) = x 2 − 2 Re ⁡ ( z ) x +...

{\displaystyle p(x_{1},\ldots ,x_{n})=0,} where p is a multivariate polynomial. Generally the polynomial is supposed to be irreducible. When this is not the case...