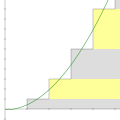
in the area of analytic number theory, the Dirichlet eta function is defined by the following Dirichlet series, which converges for any complex number...

eta function may refer to: The Dirichlet eta function η(s), a Dirichlet series The Dedekind eta function η(τ), a modular form The Weierstrass eta function...

mathematics, the Dirichlet beta function (also known as the Catalan beta function) is a special function, closely related to the Riemann zeta function. It is a...

Weierstrass eta function should not be confused with either the Dedekind eta function or the Dirichlet eta function. The Weierstrass p-function is related...

]}{\biggr \}}_{y=0}^{y=1}}={\frac {\pi }{2}}\ln(2)} The Dirichlet series defines the Dirichlet eta function as follows: η ( s ) = ∑ n = 1 ∞ ( − 1 ) n − 1 n s...

in lambda calculus. Mathematics, the Dirichlet eta function, Dedekind eta function, and Weierstrass eta function. In category theory, the unit of an adjunction...

Synchrotron function Riemann zeta function: A special case of Dirichlet series. Riemann Xi function Dirichlet eta function: An allied function. Dirichlet beta...

In mathematics, the Dedekind eta function, named after Richard Dedekind, is a modular form of weight 1/2 and is a function defined on the upper half-plane...

tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function. The Clausen function of order 2 – often referred...

zeta function Dirichlet eta function Generalized Riemann hypothesis Lehmer pair Particular values of the Riemann zeta function Prime zeta function Renormalization...

In probability and statistics, the Dirichlet distribution (after Peter Gustav Lejeune Dirichlet), often denoted Dir ⁡ ( α ) {\displaystyle \operatorname...

Approvals Dedekind eta function Dirichlet eta function Eta conversion Eta invariant Weierstrass eta function The small letter eta is used as 't Hooft...

functional equations of what are now known as the Dirichlet eta function and the Riemann zeta function. The series' terms (1, −2, 3, −4, ...) do not approach...

between the Riemann zeta function and the Dirichlet eta function η(s). The eta function is defined by an alternating Dirichlet series, so this method parallels...

Fourier series states that the Dirichlet kernel restricted to the interval [−π,π] tends to a multiple of the delta function as N → ∞. This is interpreted...

related to Dirichlet eta function and the Dirichlet beta function: Li s ⁡ ( − 1 ) = − η ( s ) , {\displaystyle \operatorname {Li} _{s}(-1)=-\eta (s),} where...

this continuation observes that the series for the zeta function and the Dirichlet eta function satisfy the relation ( 1 − 2 2 s ) ζ ( s ) = η ( s ) =...

a complex-valued arithmetic function χ : Z → C {\displaystyle \chi :\mathbb {Z} \rightarrow \mathbb {C} } is a Dirichlet character of modulus m {\displaystyle...

{\displaystyle F_{j}(0)=\eta (j+1),} where η {\displaystyle \eta } is the Dirichlet eta function. Incomplete Fermi–Dirac integral Gamma function Polylogarithm Gradshteyn...

{\displaystyle \phi } is the Euler function, η {\displaystyle \eta } is the Dedekind eta function, and the function Δ ( z ) {\displaystyle \Delta (z)}...

Euler summation to the zeta function (or rather, to the related Dirichlet eta function) yields (cf. Globally convergent series) 1 1 − 2 k + 1 ∑ i = 0 k...

1 , {\displaystyle \tau =n{\sqrt {-1}},} and Dedekind eta function η ( τ ) . {\displaystyle \eta (\tau ).} Then for n = 1 , 2 , 3 , … {\displaystyle n=1...

24 {\displaystyle \Delta =(2\pi )^{12}\eta ^{24}} where η {\displaystyle \eta } is the Dedekind eta function. For the Fourier coefficients of Δ {\displaystyle...

generalization of the Dirichlet eta function. They also later used the eta invariant of a self-adjoint operator to define the eta invariant of a compact...

Landau–Kolmogorov inequality Landau–Ramanujan constant Landau's problem on the Dirichlet eta function Landau kernel Endmund Landau (1895). "Zur relativen Wertbemessung...

distribution Dirichlet divisor problem (currently unsolved) (Number theory) Dirichlet eigenvalue Dirichlet's ellipsoidal problem Dirichlet eta function (number...

{x}{2}}\right)}^{2m+\alpha }} where Γ(z) is the gamma function. If s is a complex number, the Dirichlet eta function is formed as an alternating series η ( s ) =...

{1}{n^{s}}}=\Phi (1,s,1)} The Dirichlet eta function: η ( s ) = ∑ n = 1 ∞ ( − 1 ) n − 1 n s = Φ ( − 1 , s , 1 ) {\displaystyle \eta (s)=\sum _{n=1}^{\infty...

transform (in which he gave a first solution to Landau's problem on the Dirichlet eta function), An introduction to transform theory, and The convolution transform...

developed an algorithm that applies Chebyshev polynomials to the Dirichlet eta function to produce a very rapidly convergent series suitable for high precision...