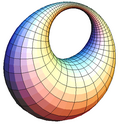
In mathematics, a Dupin cyclide or cyclide of Dupin is any geometric inversion of a standard torus, cylinder or double cone. In particular, these latter...

particularly known for work in the field of mathematics, where the Dupin cyclide and Dupin indicatrix are named after him; and for his work in the field of...

the re-inversion, this torus becomes a Dupin cyclide (Figure 3). The envelope of Soddy's hexlets is a Dupin cyclide, an inversion of the torus. Thus Soddy's...

Gaston Darboux who studied these surfaces in 1880, Darboux cyclides are a superset of Dupin cyclides and quadrics. These surfaces have applications in architectural...

sheets (purple). A Dupin cyclide and its parallels are determined by a pair of focal conic sections. The diagram shows a ring cyclide together with its...

torus Angenent torus Annulus (geometry) Clifford torus Complex torus Dupin cyclide Elliptic curve Irrational winding of a torus Joint European Torus Klein...

curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius. Lie sphere geometry...

of circles. The inversion of a cylinder, cone, or torus results in a Dupin cyclide. A spheroid is a surface of revolution and contains a pencil of circles...

Clebsch cubic Monkey saddle (saddle-like surface for 3 legs.) Torus Dupin cyclide (inversion of a torus) Whitney umbrella Right conoid (a ruled surface)...

Clebsch cubic Monkey saddle (saddle-like surface for 3 legs.) Torus Dupin cyclide (inversion of a torus) Whitney umbrella Boy's surface Cantor tree surface...

Parabolic conoid Plücker's conoid Whitney umbrella Châtelet surfaces Dupin cyclides, inversions of a cylinder, torus, or double cone in a sphere Gabriel's...

corresponding Steiner chain. The envelope of the hexlet spheres is a Dupin cyclide, the inversion of a torus. The six spheres are not only tangent to the...

particularly known for work in the field of mathematics, where the Dupin cyclide and Dupin indicatrix are named after him; and for his work in the field of statistical...

directrices for generating Dupin cyclides as canal surfaces in two ways. Focal conics can be seen as degenerate focal surfaces: Dupin cyclides are the only surfaces...

the Cretaceous and Tertiary Charles Dupin (1784–1873) – mathematician who discovered the Dupin cyclide and the Dupin indicatrix Stephan Endlicher (1804–1849)...

axis of rotation. The focal surface of a Dupin cyclide consists of a pair of focal conics. The Dupin cyclides are the only surfaces, whose focal surfaces...

analogues of Möbius transformations for oriented projective geometry Dupin cyclides, shapes obtained from cylinders and tori by inversion At the time of...

knot. Its directrix is a curve on a torus e) The 5. picture shows a Dupin cyclide (canal surface). Geometry and Algorithms for COMPUTER AIDED DESIGN,...

curvature of curves and surfaces, including surfaces of revolution, Dupin cyclides, helicoids, and minimal surfaces including the Enneper surface, with...

field is finite, then it is said to be an arithmetic quartic surface. Dupin cyclides The Fermat quartic, given by x4 + y4 + z4 + w4 =0 (an example of a K3...

with Frank Morley at Johns Hopkins University. Her thesis was titled "Dupin's cyclide as a self-dual surface". With her doctoral degree, Young was eventually...