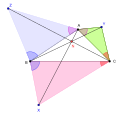
A simple proof of Jacobi's theorem   written by Kostas Vittas Fermat-Torricelli generalization at Dynamic Geometry Sketches First interactive...

matrix Jacobi's four-square theorem, in number theory Jacobi's theorem (geometry), on concurrent lines associated with any triangle Jacobi's theorem on the...

the Abel–Jacobi map is a construction of algebraic geometry which relates an algebraic curve to its Jacobian variety. In Riemannian geometry, it is a...

In geometry, the four-vertex theorem states that the curvature along a simple, closed, smooth plane curve has at least four local extrema (specifically...

differential equations and Riemannian geometry. In the theory of differential equations, comparison theorems assert particular properties of solutions...

In differential geometry, a field in mathematics, Darboux's theorem is a theorem providing a normal form for special classes of differential 1-forms, partially...

In mathematics, the Torelli theorem, named after Ruggiero Torelli, is a classical result of algebraic geometry over the complex number field, stating that...

The Carathéodory–Jacobi–Lie theorem is a theorem in symplectic geometry which generalizes Darboux's theorem. Let M be a 2n-dimensional symplectic manifold...

(algebraic geometry) Abel–Jacobi theorem (algebraic geometry) Abhyankar–Moh theorem (algebraic geometry) Addition theorem (algebraic geometry) Andreotti–Frankel...

geometry topics Glossary of Riemannian and metric geometry What follows is an incomplete list of the most classical theorems in Riemannian geometry....

later in Carl Gustav Jacobi's and William Rowan Hamilton's formulations of classical mechanics. By contrast with Riemannian geometry, where the curvature...

normal curve Conics, Pascal's theorem, Brianchon's theorem Twisted cubic Elliptic curve, cubic curve Elliptic function, Jacobi's elliptic functions, Weierstrass's...

In Riemannian geometry, a Jacobi field is a vector field along a geodesic γ {\displaystyle \gamma } in a Riemannian manifold describing the difference...

the Gauss–Codazzi equations. A major theorem, often called the fundamental theorem of the differential geometry of surfaces, asserts that whenever two...

from algebraic geometry, such as the Brill–Noether theorem or computing Gromov–Witten invariants, using the tools of tropical geometry. The basic ideas...

in Diophantine geometry since the mid-1960s, with results such as the Coates–Wiles theorem, Gross–Zagier theorem and Kolyvagin's theorem. Canonical height...

geodesics on Riemannian manifolds, Jacobi fields, the Morse index, the Rauch comparison theorems, and the Cartan–Hadamard theorem. Then it ascends to complex...

differential geometry Line element Curvature Radius of curvature Osculating circle Curve Fenchel's theorem Theorema egregium Gauss–Bonnet theorem First fundamental...

semialgebraic set: this is the Tarski–Seidenberg theorem. Related fields are o-minimal theory and real analytic geometry. Examples: Real plane curves are examples...

In Riemannian geometry, the Rauch comparison theorem, named after Harry Rauch, who proved it in 1951, is a fundamental result which relates the sectional...

coordinates is available in the mathematical setting of symplectic geometry. Liouville's theorem ignores the possibility of chemical reactions, where the total...

transformations of a group action on a smooth manifold. The third theorem on the list stated the Jacobi identity for the infinitesimal transformations of a local...

is experiencing spherical pulsations. Then Birkhoff's theorem says that the exterior geometry must be Schwarzschild; the only effect of the pulsation...

gravitation produces singularities. The Penrose singularity theorem is a theorem in semi-Riemannian geometry and its general relativistic interpretation predicts...

principal ideas of geometric mechanics is reduction, which goes back to Jacobi's elimination of the node in the 3-body problem, but in its modern form is...

In differential geometry, the last geometric statement of Jacobi is a conjecture named after Carl Gustav Jacob Jacobi, which states: Every caustic from...

Some theorems of Riemannian geometry can be generalized to the pseudo-Riemannian case. In particular, the fundamental theorem of Riemannian geometry is...

optico-mechanical analogy. In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the...

1848 and known as the Gauss–Bonnet theorem. During Gauss' lifetime, the Parallel postulate of Euclidean geometry was heavily discussed. Numerous efforts...

generalization includes generalizations of the inverse function theorem and the implicit function theorem, where the non-nullity of the derivative is replaced by...