analytic geometry, a line and a sphere can intersect in three ways: No intersection at all Intersection in exactly one point Intersection in two points. Methods...

geometric intersection include: Line–plane intersection Line–sphere intersection Intersection of a polyhedron with a line Line segment intersection Intersection...

Line-cylinder intersection is the calculation of any points of intersection, given an analytic geometry description of a line and a cylinder in 3d space...

apply to the sphere. A particular line passing through its center defines an axis (as in Earth's axis of rotation). The sphere-axis intersection defines two...

geometric intersection include: Line–plane intersection Line–sphere intersection Intersection of a polyhedron with a line Line segment intersection Intersection...

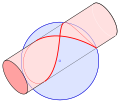
the Dandelin spheres are one or two spheres that are tangent both to a plane and to a cone that intersects the plane. The intersection of the cone and...

projective geometry, the sphere is an example of a complex projective space and can be thought of as the complex projective line P 1 ( C ) {\displaystyle...

lesser circles. If the sphere is embedded in three-dimensional Euclidean space, its circles are the intersections of the sphere with planes, and the great...

circular intersection of a sphere and a plane passing through the sphere's center point. Any arc of a great circle is a geodesic of the sphere, so that...

consider how one would find the intersection between a ray and a sphere. This is merely the math behind the line–sphere intersection and the subsequent determination...

determine the intersection points of a line with a quadric (i.e. line-sphere); one only has to solve a quadratic equation. So, any intersection curve of a...

Any plane passing through O, inverts to a sphere touching at O. A circle, that is, the intersection of a sphere with a secant plane, inverts into a circle...

possible to smoothly and continuously turn a sphere inside out in this way (allowing self-intersections of the sphere's surface) without cutting or tearing it...

hyperplane is a 2-sphere (unless the hyperplane is tangent to the 3-sphere, in which case the intersection is a single point). As a 3-sphere moves through...

intersection of a small 3-sphere around 0 with this complex surface) is a Brieskorn manifold that is a homology 3-sphere, called a Brieskorn 3-sphere...

swept sphere and the segment that the sphere is swept across). It has traits similar to a cylinder, but is easier to use, because the intersection test...

by a point on a circle or sphere, the intersection between the sphere and a ray in that direction emanating from the sphere's center; the tips of unit...

mass of a triangle must be at the intersection point of the medians. For the triangle in question, one median is the line y = x / 2 {\displaystyle y=x/2}...

1590s. A rhumb line can be contrasted with a great circle, which is the path of shortest distance between two points on the surface of a sphere. On a great...

armillary sphere (variations are known as spherical astrolabe, armilla, or armil) is a model of objects in the sky (on the celestial sphere), consisting...

or two points in the intersection of a line and a circle (if they intersect) Creating the one or two points in the intersection of two circles (if they...

In the extrinsic 3-dimensional picture, a great circle is the intersection of the sphere with any plane through the center. In the intrinsic approach,...

common. In the last case, the three lines of intersection of each pair of planes are mutually parallel. A line can lie in a given plane, intersect that plane...

a polygon on the surface of the sphere. Its sides are arcs of great circles—the spherical geometry equivalent of line segments in plane geometry. Such...

defined by the intersection with the sphere of a horizontal plane located at any height y {\displaystyle y} equals the area of the intersection of that plane...

connecting the spheres enclose stairs, escalators and a lift (in the central, vertical tube) to allow access to the six visitable spheres, which contain...

It is the intersection of a sphere with a cylinder that is tangent to the sphere and passes through two poles (a diameter) of the sphere (see diagram)...

a line through O, one can conclude that any pair of lines in the extension intersect: the point of intersection lies where the plane intersection meets...

a circle on the celestial sphere, and its rays striking the point on a sundial traces out a cone of light. The intersection of this cone with the horizontal...

intersection points of each of the three pairs of external tangent lines are collinear. For any two circles in a plane, an external tangent is a line...