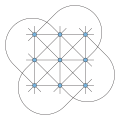
triangular edges. Coxeter named it a Möbius–Kantor polygon for sharing the complex configuration structure as the Möbius–Kantor configuration, (83). Discovered...
5 KB (459 words) - 00:15, 27 March 2025
the complex polygon 3{3}3. Coxeter named it a Möbius–Kantor polygon. More abstractly, the Möbius–Kantor configuration can be described as a system of...
9 KB (1,009 words) - 02:28, 20 October 2023
the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor. It...
13 KB (1,529 words) - 12:57, 26 February 2025
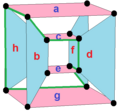
16-cell (section Related complex polygons)
16-cell can be seen as its dual, a 4-4 duopyramid. The Möbius–Kantor polygon is a regular complex polygon 3{3}3, , in C 2 {\displaystyle \mathbb {C} ^{2}} shares...
61 KB (7,127 words) - 18:16, 16 April 2025
hyperplanes of symmetry passing through the center yield complex 3{4}3 Möbius–Kantor polygons. The root vectors of simple Lie group E8 are represented by the...
15 KB (2,028 words) - 18:26, 11 April 2025
Incidence geometry (section Möbius planes)
through that point (but not the other points on them) produces the (83) Möbius–Kantor configuration. Given an integer α ≥ 1, a tactical configuration satisfying:...
27 KB (3,321 words) - 07:34, 29 August 2023
In geometry, a regular complex polygon is a generalization of a regular polygon in real space to an analogous structure in a complex Hilbert space, where...
37 KB (1,846 words) - 08:53, 28 November 2024
configuration, (123 94), points indexed 1...12 can have configuration table: Möbius–Kantor configuration Removing any one point and its four incident lines from...
12 KB (1,360 words) - 07:51, 2 May 2025
Complex polytope (redirect from Van Oss polygon)
polygon is a truncation of a regular polygon. A quasiregular polygon contains alternate edges of the regular polygons and . The quasiregular polygon has...
154 KB (6,983 words) - 07:42, 7 April 2025
geometry, but cannot be constructed in the Euclidean plane. (83), the Möbius–Kantor configuration. This configuration describes two quadrilaterals that...
16 KB (1,692 words) - 01:46, 8 May 2025
Petersen graphs are the n-prism G(n, 1), the Dürer graph G(6, 2), the Möbius-Kantor graph G(8, 3), the dodecahedron G(10, 2), the Desargues graph G(10,...
13 KB (1,397 words) - 11:53, 26 January 2025
strongly regular graph is symmetric, but not vice versa. Heawood graph Möbius–Kantor graph Pappus graph Desargues graph Nauru graph Coxeter graph Tutte–Coxeter...
14 KB (1,251 words) - 14:50, 13 March 2024
{\displaystyle G(n,1)} the Dürer graph G ( 6 , 2 ) {\displaystyle G(6,2)} , the Möbius-Kantor graph G ( 8 , 3 ) {\displaystyle G(8,3)} , the dodecahedron G ( 10 ...
24 KB (2,993 words) - 04:57, 12 April 2025
graphs are the cubical graph G(4, 1), the Petersen graph G(5, 2), the Möbius–Kantor graph G(8, 3), the dodecahedral graph G(10, 2) and the Nauru graph G(12...
10 KB (1,203 words) - 11:19, 3 August 2024
by connecting an outer polygon and an inner star with the same number of points; for instance, this applies to the Möbius–Kantor graph and the Desargues...
4 KB (450 words) - 15:10, 2 December 2023
^{3}} contains 72 regular complex triangular edges, as well as 27 polygonal Möbius–Kantor faces and 27 vertices. It is notable for being the vertex figure...
15 KB (2,071 words) - 12:41, 21 April 2025
unit distance graphs). All generalized Petersen graphs, such as the Möbius–Kantor graph depicted, are non-strict unit distance graphs. Matchstick graphs...
33 KB (4,019 words) - 07:16, 22 November 2024
G(4,1)} , the Petersen graph G ( 5 , 2 ) {\displaystyle G(5,2)} , the Möbius–Kantor graph G ( 8 , 3 ) {\displaystyle G(8,3)} , the dodecahedral graph G...
11 KB (1,378 words) - 20:54, 8 February 2025