In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices. It collects the various...

the product of the Jones matrix of the optical element and the Jones vector of the incident light. Note that Jones calculus is only applicable to light...

In vector calculus, the Jacobian matrix (/dʒəˈkoʊbiən/, /dʒɪ-, jɪ-/) of a vector-valued function of several variables is the matrix of all its first-order...

vector field Laplacian Laplacian vector field Level set Line integral Matrix calculus Mixed derivatives Monkey saddle Multiple integral Newtonian potential...

Orthonormalization of a set of vectors Irregular matrix Matrix calculus – Specialized notation for multivariable calculus Matrix function – Function that maps matrices...

In mathematics, the Hessian matrix, Hessian or (less commonly) Hesse matrix is a square matrix of second-order partial derivatives of a scalar-valued function...

theory, the Laplacian matrix, also called the graph Laplacian, admittance matrix, Kirchhoff matrix, or discrete Laplacian, is a matrix representation of a...

inner-product space Matrix calculus, a specialized notation for multivariable calculus over spaces of matrices Numerical calculus (also called numerical...

Mueller calculus is a matrix method for manipulating Stokes vectors, which represent the polarization of light. It was developed in 1943 by Hans Mueller...

columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number...

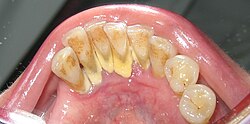
in the early 19th century. Calculus is composed of both inorganic (mineral) and organic (cellular and extracellular matrix) components. The mineral proportion...

integration Gabriel's horn Jacobian matrix Hessian matrix Curvature Green's theorem Divergence theorem Stokes' theorem Vector Calculus Infinite series Maclaurin...

the Hessian matrix at these zeros. Vector calculus can also be generalized to other 3-manifolds and higher-dimensional spaces. Vector calculus is initially...

transpose of a matrix is an operator which flips a matrix over its diagonal; that is, it switches the row and column indices of the matrix A by producing...

used to be called the absolute differential calculus (the foundation of tensor calculus), tensor calculus or tensor analysis developed by Gregorio Ricci-Curbastro...

functions to a square matrix, extending what has just been discussed. In the finite-dimensional case, the polynomial functional calculus yields quite a bit...

matrices such that A B is a square matrix. The Frobenius inner product and norm arise frequently in matrix calculus and statistics. The Frobenius inner...

collecting statistical data. Mathematical system theory Matrix algebra Matrix calculus Matrix theory Matroid theory Measure theory Metric geometry Microlocal...

Multivariable calculus (also known as multivariate calculus) is the extension of calculus in one variable to calculus with functions of several variables:...

cross-vector. Dyadics Householder transformation Norm (mathematics) Ricci calculus Scatter matrix Cartesian product Cross product Exterior product Hadamard product...

Baksalary, Oskar Maria (2023). "Professor Heinz Neudecker and matrix differential calculus". Statistical Papers. 65 (4): 2605–2639. doi:10.1007/s00362-023-01499-w...

matrix, binary matrix, relation matrix, Boolean matrix, or (0, 1)-matrix is a matrix with entries from the Boolean domain B = {0, 1}. Such a matrix can...

especially in linear algebra and matrix theory, the vectorization of a matrix is a linear transformation which converts the matrix into a vector. Specifically...

The fundamental theorem of calculus is a theorem that links the concept of differentiating a function (calculating its slopes, or rate of change at every...

differences. The study of differential calculus is unified with the calculus of finite differences in time scale calculus. The arithmetic derivative involves...

called infinitesimal calculus or "the calculus of infinitesimals", it has two major branches, differential calculus and integral calculus. The former concerns...

square matrix. The determinant of a matrix A is commonly denoted det(A), det A, or |A|. Its value characterizes some properties of the matrix and the...

In vector calculus, the gradient of a scalar-valued differentiable function f {\displaystyle f} of several variables is the vector field (or vector-valued...

units) The equations of motion derived by extremizing the action (see matrix calculus for the notation): d P d t = ∂ L ∂ r = q ∂ A ∂ r ⋅ r ˙ − q ∂ ϕ ∂ r...

the derivatives of the rotated quaternion can be represented using matrix calculus notation as ∂ p ′ ∂ q ≡ [ ∂ p ′ ∂ q 0 , ∂ p ′ ∂ q x , ∂ p ′ ∂ q y ...