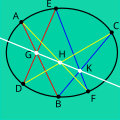
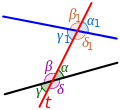
In Euclidean geometry, Menelaus's theorem, named for Menelaus of Alexandria, is a proposition about triangles in plane geometry. Suppose we have a triangle...

{CE}}{\overline {EA}}}\right|=1,} as required. The theorem can also be proven easily using Menelaus's theorem. From the transversal BOE of triangle △ACF, A...

St Andrews "Book 3 deals with spherical trigonometry and includes Menelaus's theorem". Kennedy, E. S. (1969). "The History of Trigonometry". 31st Yearbook...

result based on areas or wedge products or, as the following proof, on Menelaus's theorem, due to Hillyer and published in 1920. Let the complete quadrilateral...

triangle A B D {\displaystyle ABD} and line F R C {\displaystyle FRC} , Menelaus's theorem implies A F F B × B C C D × D R R A = − 1 {\displaystyle {\frac {AF}{FB}}\times...

Kawasaki's theorem (mathematics of paper folding) Lester's theorem (Euclidean plane geometry) Lexell's theorem (spherical geometry) Menelaus's theorem (geometry)...

depend on the angles of the triangle, such as Ceva's theorem, Routh's theorem, and Menelaus's theorem. In computer-aided design, they are useful for defining...

three dimensions. Monge's theorem can also be proved by using Desargues' theorem. Another easy proof uses Menelaus' theorem, since the ratios can be calculated...

In projective geometry, Pascal's theorem (also known as the hexagrammum mysticum theorem, Latin for mystical hexagram) states that if six arbitrary points...

about Menelaus's life, it is supposed that he lived in Rome, where he probably moved after having spent his youth in Alexandria. He was called Menelaus of...

Brianchon's theorem Ceva's theorem Desargues's theorem Menelaus's theorem Pascal's theorem Poncelet's closure theorem Ptolemy's theorem Apollonian circles...

are: the angle bisector theorem, the geometric mean theorem, Ceva's theorem, Menelaus's theorem and the Pythagorean theorem. Similar triangles also provide...

In geometry, Apollonius's theorem is a theorem relating the length of a median of a triangle to the lengths of its sides. It states that the sum of the...

the later tradition of Alexandria. In the Elements, Euclid deduced the theorems from a small set of axioms. He also wrote works on perspective, conic sections...

St Andrews "Book 3 deals with spherical trigonometry and includes Menelaus's theorem." Kennedy, E. S. (1969), "The History of Trigonometry", 31st Yearbook...

Hellenistic mathematician and astronomer Menelaus's theorem, a theorem attributed to Menelaus of Alexandria Jane Menelaus (born 1959), Australian actress This...

{3}{13}}={\tfrac {7}{26}}.} Cevian Ceva's theorem Menelaus's theorem Stewart's theorem Angle bisector theorem Routh's theorem Barycentric coordinates Lever Rhoad...

proving that three symmetrically constructed points are collinear; here Menelaus' theorem gives a useful general criterion. In this section, just a few of the...

was translated into Arabic with a few additions such as Euclid's Data, Menelaus's Spherics (extant in Arabic only), and various works by Archimedes as the...

fi-l-hisab al Hindi). He also wrote on Archimedes's Book of Lemmas and Menelaus's theorem (Kitab al-ishba, or "satiation"), where he made corrections to the...

equal to one. He published this theorem in De lineis rectis. Ceva also rediscovered and published Menelaus's theorem. He published Opuscula mathematica...

proven to be impossible, as a consequence of the Lindemann–Weierstrass theorem, which proves that pi ( π {\displaystyle \pi } ) is a transcendental number...

a transversal, the lengths of the six resulting segments satisfy Menelaus' theorem. Euclid's formulation of the parallel postulate may be stated in terms...

trigonometric formulas, for example Al-Nayrizi's four-step application of Menelaus's theorem. Subsequent scholars, including Ibn Yunus, Abu al-Wafa, Ibn al-Haitham...

intersections of three cevians, one from each vertex. Mass point geometry Menelaus' theorem Coxeter, H. S. M.; Greitzer, S. L. (1967). Geometry Revisited. Washington...

the sphere, and Menelaus of Alexandria, who wrote a book on spherical trigonometry called Sphaerica and developed Menelaus' theorem. The Book of Unknown...

with the excircle relative to that side are collinear.: p.120, #78  Menelaus' theorem states that three points P 1 , P 2 , P 3 {\displaystyle P_{1},P_{2}...

theory Angle bisector theorem Butterfly theorem Ceva's theorem Heron's formula Menelaus' theorem Nine-point circle Pythagorean theorem Eves 1963, p. 19. Eves...

(Cleomedes, Nicomachus, and Theon of Smyrna) XVII. Trigonometry: Hipparchus, Menelaus, Ptolemy XVIII. Mensuration: Heron of Alexandria XIX. Pappus of Alexandria...

numbers possessing square roots. Menelaus of Alexandria (c. 100 AD) pioneered spherical trigonometry through Menelaus' theorem. The most complete and influential...