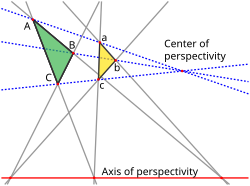
In geometry, Monge's theorem, named after Gaspard Monge, states that for any three circles in a plane, none of which is completely inside one of the others...

circle's interior. Tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...

statics. History of the metre Monge array Monge cone Monge equation Monge patch Monge point Monge–Ampère equation Monge's theorem Clebsch representation Earth...

in this case it is not possible to find a point not in the plane. Monge's theorem also asserts that three points lie on a line, and has a proof using...

Miquel's theorem (geometry) Mohr–Mascheroni theorem (geometry) Monge's theorem (geometry) Morley's trisector theorem (geometry) Napoleon's theorem (triangle...

( M 1 , M 2 ; E , I ) = − 1 {\displaystyle (M_{1},M_{2};E,I)=-1} . Monge's theorem states: The outer similarity points of three disjoint circles lie on...

circle topics Thales' theorem Circumcircle Concyclic Incircle and excircles of a triangle Orthocentric system Monge's theorem Power center Nine-point...

lie on a conic, which may be degenerate as in Pappus's hexagon theorem. By Monge's theorem, for any three circles in a plane, none of which is completely...

connecting two pulleys, in Casey's theorem characterizing sets of four circles with a common tangent circle, and in Monge's theorem on the collinearity of intersection...

differential equations, the Calabi conjecture, the positive energy theorem, and the Monge–Ampère equation. Yau is considered one of the major contributors...

Milne-Thomson circle theorem Miquel's theorem – Concerns 3 circles through triples of points on the vertices and sides of a triangle Monge's theorem – The intersections...

sufficiently close F. Calabi proved this by using the implicit function theorem for Banach spaces: in order to apply this, the main step is to show that...

of this orthogonal circle corresponds to Monge's problem. This is a special case of the three conics theorem. The three radical axes meet in a single...

{\displaystyle X} and ν {\displaystyle \nu } on Y {\displaystyle Y} , Monge's formulation of the optimal transportation problem is to find a transport...

prove the Sobolev embedding theorem, giving inclusions between certain Sobolev spaces, and the Rellich–Kondrachov theorem showing that under slightly...

In mathematics, Liouville's theorem, proved by Joseph Liouville in 1850, is a rigidity theorem about conformal mappings in Euclidean space. It states that...

In mathematics, a (real) Monge–Ampère equation is a nonlinear second-order partial differential equation of special kind. A second-order equation for...

1489–1501. doi:10.1051/cocv/2017050. (See Theorem 2.5.) Bogachev VI, Kolesnikov AV (October 2012). "The Monge–Kantorovich problem: achievements, connections...

the Schoenflies problem or Schoenflies theorem, of geometric topology is a sharpening of the Jordan curve theorem by Arthur Schoenflies. For Jordan curves...

known as theorems of Ohsawa–Takegoshi type. Suita conjecture Ohsawa & Takegoshi (1987) Siu (2011) Błocki, Zbigniew (2014). "Cauchy–Riemann meet Monge–Ampère"...

Charles Julien Brianchon provided a significant contribution to Feuerbach's theorem. He also made discoveries about projective harmonic conjugates; relating...

physicist. He was one of the first to rigorously state and prove the key theorems of calculus (thereby creating real analysis), pioneered the field complex...

Brianchon's theorem (1810). Brianchon's book Mémoire sur les lignes du second ordre (Paris, 1817) is available online [1]. Brianchon's Theorem O'Connor,...

{\displaystyle f\circ \sigma } is μ {\displaystyle \mu } -integrable. Theorem. Consider a map ξ : Ω → R d {\displaystyle \xi :\Omega \rightarrow R^{d}}...

de curvatura". Materials Matemàtics. 01: 1–25. Historical Comments on Monge's Ellipsoid and the Configuration of Lines of Curvature on Surfaces Immersed...

second-order parabolic partial differential equations and the Newlander–Nirenberg theorem in complex geometry. He is regarded as a foundational figure in the field...

two distribution functions across all x values. By the Glivenko–Cantelli theorem, if the sample comes from the distribution F(x), then Dn converges to 0...

preparation theorem. A generalization of this theorem using the same method as Hartogs was proved in 2007. From Hartogs's extension theorem the domain...

Butterfly theorem, Angle bisector theorem, Apollonius' theorem, British flag theorem, Ceva's theorem, Equal incircles theorem, Geometric mean theorem, Heron's...

the foundations of geometry. Pogorelov's uniqueness theorem and the Alexandrov–Pogorelov theorem are named after him. He was born in Korocha in a peasant...