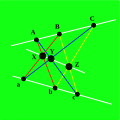
containing the three intersection points X, Y, and Z, called the Pappus line. The Pappus configuration can also be derived from two triangles △XcC and △YbB that...

Alexandria Pappus's centroid theorem, another theorem named for Pappus of Alexandria Pappus configuration, a geometric configuration related to 'Pappus's theorem'...

In mathematics, Pappus's hexagon theorem (attributed to Pappus of Alexandria) states that given one set of collinear points A , B , C , {\displaystyle...

three different (93 93) configurations: the Pappus configuration and two less notable configurations. In some configurations, p = ℓ and consequently,...

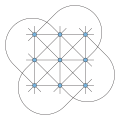
the Pappus graph is a bipartite, 3-regular, undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is...

vertices. The Pappus graph is the Levi graph of the Pappus configuration, composed of 9 points and 9 lines. Like the Desargues configuration there are 3...

\left[{\begin{smallmatrix}9&3\\3&9\\\end{smallmatrix}}\right]} , the Pappus configuration. The Pappus configuration has 18×3! = 108 automorphisms. Dual of K3,3 graph Removing...

Gergonne, Steiner and Poncelet. Pappus's hexagon theorem Pappus's centroid theorem Pappus chain Pappus configuration Pappus graph Bird, John (14 July 2017)...

and one point on four lines. In this respect it differs from the Pappus configuration, which also has nine points and nine lines, but with three points...

the Pappus configuration. The Reye configuration is formed by four quadruply perspective tetrahedra in an analogous way to the Pappus configuration. Curvilinear...

is Pappus of Alexandria (4th century AD). He is known for his hexagon theorem and centroid theorem, as well as the Pappus configuration and Pappus graph...

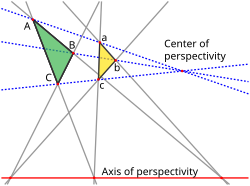
the non-existence of hidden variables in quantum mechanics. The Pappus configuration may be formed from two triangles that are perspective figures to...

Non-uniform structure 3. Generalized quadrangle 4. Möbius–Kantor configuration 5. Pappus configuration An incidence structure is uniform if each line is incident...

problem) asks for the maximum number of 3-point lines attainable by a configuration of a specific number of points in the plane. There are also investigations...

Victor; Schacht, Celia (2019), "The axiomatic destiny of the theorems of Pappus and Desargues", in Dani, S. G.; Papadopoulos, A. (eds.), Geometry in history...

p. 52) Pappus 1.   Pappus of Alexandria. 2.  The Pappus configuration is the configuration of 9 lines and 9 points that occurs in Pappus's hexagon theorem...

forming a configuration of this type. This incidence theorem is true more generally in a three-dimensional projective space if and only if Pappus's theorem...

deals with parallel lines, one of the properties of parallels noted by Pappus of Alexandria has been taken as a premise: Suppose A, B, C are on one line...

now-lost work. Although they were not credited to Archimedes originally, Pappus of Alexandria in the fifth section of his titled compendium Synagoge referring...

been lost, and is known largely through a description of its contents by Pappus of Alexandria and through fragmentary references to it in medieval Islamic...

points of the other. It is the Levi graph of the Desargues configuration. This configuration consists of ten points and ten lines describing two perspective...

generalizations of Steiner chains exist, most notably Soddy's hexlet and Pappus chains. Steiner chains with different internal/external tangencies The 7...

cross-ratio. Pappus of Alexandria made implicit use of concepts equivalent to the cross-ratio in his Collection: Book VII. Early users of Pappus included...

of fundamental importance include Desargues' Theorem and the Theorem of Pappus. In projective spaces of dimension 3 or greater there is a construction...

of separated vortex rings (SVR) such as those formed in the wake of the pappus of a dandelion. This special type of vortex ring effectively stabilizes...

inscribed in the same sphere. The problem was solved by Hero of Alexandria, Pappus of Alexandria, and Fibonacci, among others. Apollonius of Perga discovered...

n-torus is the configuration space of n ordered, not necessarily distinct points on the circle. Symbolically, Tn = (S1)n. The configuration space of unordered...

the original (PDF) on 2008-04-15. Retrieved 2009-04-16. Pappus of Alexandria (1933). Pappus d'Alexandrie: La collection mathématique (in French). Paris...

dodecahedron inscribed in the same sphere. The problem was solved by Hero, Pappus, and Fibonacci, among others. Apollonius of Perga discovered the curious...

lost work. All that is now known of his work on these shapes comes from Pappus of Alexandria, who merely lists the numbers of faces for each: 12 pentagons...