In combinatorics, a branch of mathematics, partition regularity is one notion of largeness for a collection of sets. Given a set X {\displaystyle X} ,...

In extremal graph theory, Szemerédi’s regularity lemma states that a graph can be partitioned into a bounded number of parts so that the edges between...

of Regularity, also called the Axiom of Foundation, an axiom of set theory asserting the non-existence of certain infinite chains of sets Partition regularity...

pieces has a given interesting property? This idea can be defined as partition regularity. For example, consider a complete graph of order n; that is, there...

the random-like parts. This is an extension of Szemerédi's regularity lemma that partitions any given graph into bounded number parts such that edges between...

algorithmic version of the Szemerédi regularity lemma to find an ϵ {\displaystyle \epsilon } -regular partition. Lemma 1: Fix k and γ {\displaystyle \gamma...

{N} } , the Stone–Čech compactification of the natural numbers. Partition regularity: if S {\displaystyle S} is piecewise syndetic and S = C 1 ∪ C 2 ∪...

simplest forms, the graph counting lemma uses regularity between pairs of parts in a regular partition to approximate the number of subgraphs, and the...

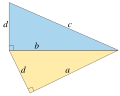
on 2013-01-20 Cooper, Joshua; Poirel, Chris (2008), Pythagorean partition-regularity and ordered triple systems with the sum property, arXiv:0809.3478...

"Extremal Sidon Sets are Fourier Uniform, with Applications to Partition Regularity". Journal de théorie des nombres de Bordeaux. 35 (1): 115–134. arXiv:2110...

theorem. The axiom of choice is equivalent to the statement that every partition has a transversal. In many cases, a set created by choosing elements can...

b {\displaystyle a,b,a^{b}} is monochromatic, demonstrating the partition regularity of complex exponential patterns. This work marks a crucial development...

\mathbb {N} } . This theorem highlights the relationship between the partition regularity of the natural numbers and ultrafilters, offering a fundamental result...

{\displaystyle E} as an instrument to split A {\displaystyle A} into two partitions: the part of A {\displaystyle A} which intersects with E {\displaystyle...

schema of replacement. Appending this schema, as well as the axiom of regularity (first proposed by John von Neumann), to Zermelo set theory yields the...

preregularity, rather than regularity, that matters in these situations. However, definitions are usually still phrased in terms of regularity, since this condition...

{\displaystyle a=c} (transitive). Each equivalence relation provides a partition of the underlying set into disjoint equivalence classes. Two elements...

given closed support are used in the construction of smooth partitions of unity (see partition of unity and topology glossary); these are essential in the...

monochromatic, may be seen as a special case of Rado's theorem concerning the regularity of the system of equations x T = ∑ i ∈ T x { i } , {\displaystyle x_{T}=\sum...

{\mathcal {P}}} . The statement that a graph G {\displaystyle G} has a regularity partition is equivalent to saying that its associated graphon W G {\displaystyle...

comprehension, or the axiom of regularity and axiom of pairing. In Zermelo–Fraenkel set theory, the axiom of regularity and axiom of pairing prevent any...

be the energy function defined in Szemerédi regularity lemma. Essentially, we can find a pair of partitions P , Q {\displaystyle {\mathcal {P}},{\mathcal...

Therefore, it is not possible to strengthen the regularity lemma to show the existence of a partition for which all pairs are regular. On the other hand...

quasi-conformal...), a manifold of that regularity is a topological manifold whose charts transitions have the prescribed regularity. Manifold with boundary Manifold...

G_{l}^{(2)}} via a partition of the vertex set. As a result, we have the total data of hypergraph regularity as follows: a partition of E ( K n ) {\displaystyle...

are partitioned into finitely many subsets, there exist arbitrarily large sets of numbers all of whose sums belong to the same subset of the partition. The...

candidate u to the data f. The parameter γ > 0 controls the tradeoff between regularity and data fidelity. There are fast algorithms for the exact minimization...

, and therefore, yes, c > log b ⁡ a {\displaystyle c>\log _{b}a} The regularity condition also holds: 2 ( n 2 4 ) ≤ k n 2 {\displaystyle 2\left({\frac...

analytic methods. Later on another proof was given using Szemerédi's regularity lemma. In 1953, Roth used Fourier analysis to prove an upper bound of...

of the largest independent set is equal to the number of cliques in a partition of the graph's vertices into a minimum number of cliques. In a rook's...