coefficients is known as Pascal's rule. The pattern of numbers that forms Pascal's triangle was known well before Pascal's time. The Persian mathematician...

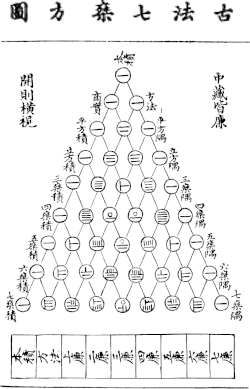
mathematics, Pascal's pyramid is a three-dimensional arrangement of the coefficients of the trinomial expansion and the trinomial distribution. Pascal's pyramid...

"Pascal's Triangle Revisited" is the twenty-fifth and final episode of the first season of Community. It originally aired in the United States on NBC...

{\displaystyle i} . A generalization of the Sierpiński triangle can also be generated using Pascal's triangle if a different modulus P {\displaystyle P} is used...

sides lie on a line (called the Pascal line). Pascal's work was so precocious that René Descartes was convinced that Pascal's father had written it. When...

{\displaystyle n} ⁠ and ⁠ k {\displaystyle k} ⁠ can be arranged to form Pascal's triangle. These numbers also occur in combinatorics, where ⁠ ( n k ) {\displaystyle...

left and right of Pascal's triangle, the entries (shown as blanks) are all zero. Pascal's rule also gives rise to Pascal's triangle: Row number n contains...

_{k=0}^{n-r}{\binom {r+k}{r}}={\binom {n+1}{r+1}}} Pascal's identity Pascal's triangle Leibniz triangle Vandermonde's identity Faulhaber's formula, for sums...

One can use the multinomial theorem to generalize Pascal's triangle or Pascal's pyramid to Pascal's simplex. This provides a quick way to generate a lookup...

Is there some constant N such that every entry (apart from 1) of Pascal's triangle appears fewer than N times? More unsolved problems in mathematics...

\5&&1&6&16&26&31&32\end{array}}} Similarly to Pascal's triangle, each component of Bernoulli's triangle is the sum of two components of the previous row...

written in binary, are equal to the first 32 rows of the modulo-2 Pascal's triangle, minus the top row, which corresponds to a monogon. (Because of this...

Connection with Worpitzky numbers). There are formulas connecting Pascal's triangle to Bernoulli numbers B n + = | A n | ( n + 1 ) !       {\displaystyle...

depict Pascal's triangle: Pascal ← {' '@(0=⊢)↑0,⍨¨a⌽¨⌽∊¨0,¨¨a∘!¨a←⌽⍳⍵} ⍝ Create a one-line user function called Pascal Pascal 7 ⍝ Run function Pascal for...

since they show up exactly in the middle of the even-numbered rows in Pascal's triangle. The first few central binomial coefficients starting at n = 0 are:...

Henry W. Gould that counts how many odd numbers are in each row of Pascal's triangle. It consists only of powers of two, and begins: 1, 2, 2, 4, 2, 4,...

one-dimensional (1D) slices of Pascal's triangle, so too can one interpret the multinomial distribution as 2D (triangular) slices of Pascal's pyramid, or 3D/4D/+...

for his contribution of presenting Yang Hui's triangle. This triangle was the same as Pascal's triangle, discovered by Yang's predecessor Jia Xian. Yang...

In mathematics, Pascal's rule (or Pascal's formula) is a combinatorial identity about binomial coefficients. The binomial coefficients are the numbers...

the Duke of Zhou. Knowledge of Pascal's triangle has also been shown to have existed in China centuries before Pascal, such as the Song-era polymath Shen...

sometimes called generalized Pascal triangles; examples include Pascal's triangle, the Narayana numbers, and the triangle of Eulerian numbers. Triangular...

alternatively derived from the sum of up to the first 3 terms of each row of Pascal's triangle: This sequence (sequence A000124 in the OEIS), starting with n = 0...

a Pascal matrix is a matrix (possibly infinite) containing the binomial coefficients as its elements. It is thus an encoding of Pascal's triangle in...

in his paper The Scales of Mt. Meru observed certain diagonals in Pascal's triangle (see diagram) and drew them on paper in 1993. The Padovan numbers...

appropriate binomial coefficients. Tartaglia knew of Pascal's triangle one hundred years before Pascal, as shown in this image from the General Trattato...

Only three such pairs of numbers are known.[citation needed] Rows in Pascal's triangle can be seen as representation of powers of 11. An 11-sided polygon...

around 1300. Today, this triangle is known as Pascal's triangle. Pascal's contribution to the triangle that bears his name comes from his work on formal...

(1 + X)n = (1 + X)n − 1(1 + X); this leads to the construction of Pascal's triangle. For determining an individual binomial coefficient, it is more practical...

entries of this triangle can be computed from Pascal's: "The terms in each row are the initial term divided by the corresponding Pascal triangle entries." In...

sequences are given by the binomial coefficients along any row of Pascal's triangle and the elementary symmetric means of a finite sequence of real numbers...