quantum mechanics, the projective Hilbert space or ray space P ( H ) {\displaystyle \mathbf {P} (H)} of a complex Hilbert space H {\displaystyle H} is...

inequality for complex projective space Projective Hilbert space Quaternionic projective space Real projective space Complex affine space K3 surface Besse,...

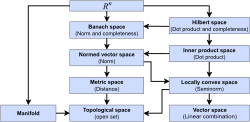
In mathematics, a Hilbert space is a real or complex inner product space that is also a complete metric space with respect to the metric induced by the...

transition probability. Ray space, in mathematics known as projective Hilbert space, is the space of all unit vectors in Hilbert space up to the equivalence...

mathematics, a Hilbert scheme is a scheme that is the parameter space for the closed subschemes of some projective space (or a more general projective scheme)...

the dimension of the Hilbert space and pure states can be represented as equivalence classes, or, rays in a projective Hilbert space P ( H n ) = C P n −...

When the setting for random variables is on complex projective space or projective Hilbert space, geometrized with the Fubini–Study metric, the theory...

In algebraic geometry, a projective variety is an algebraic variety that is a closed subvariety of a projective space. That is, it is the zero-locus in...

properly speaking, a point in the projective Hilbert space corresponds to a line passing through the origin of the Hilbert space, rather than a half-line, or...

induced by the flat space Euclidean metric, after appropriate changes of variable. When extended to complex projective Hilbert space, it becomes the Fubini–Study...

Technically, wave functions form a ray in a projective Hilbert space rather than an ordinary vector space. At a particular instant of time, all values...

In mathematics, the Hilbert metric, also known as the Hilbert projective metric, is an explicitly defined distance function on a bounded convex subset...

defining a projective space as the set of the vector lines in a vector space of dimension one more. As for affine spaces, projective spaces are defined...

compared to elementary Euclidean geometry, projective geometry has a different setting (projective space) and a selective set of basic geometric concepts...

point", which is subject to the axioms of projective geometry. For some such set of axioms, the projective spaces that are defined have been shown to be...

series and the Hilbert polynomial of a filtered algebra are those of the associated graded algebra. The Hilbert polynomial of a projective variety V in...

the lines of the projective space are geodesics. Metrics of this type are called flat or projective. Thus, the solution of Hilbert's fourth problem was...

mathematics, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear group P...

simple example of a Hilbert scheme is the Hilbert scheme parameterizing degree d {\displaystyle d} hypersurfaces of projective space P n {\displaystyle...

Projective connection Projective Hilbert space Projective morphism Projective polyhedron Projective resolution Projective test Projective techniques Projection...

"Banach space" and Banach in turn then coined the term "Fréchet space". Banach spaces originally grew out of the study of function spaces by Hilbert, Fréchet...

subsets of projective space. Projective varieties were subsets defined by a set of homogeneous polynomials. At each point of the projective variety, all...

The projective nature of quantum-mechanical-state space causes some confusion, because a quantum mechanical state is a ray in projective Hilbert space, not...

a Hilbert space does not suffice for defining coordinates as wave functions form rays in a projective Hilbert space (rather than an ordinary Hilbert space)...

Hilbert's fifth problem is the fifth mathematical problem from the problem list publicized in 1900 by mathematician David Hilbert, and concerns the characterization...

properties. Nuclear spaces are however quite different from Hilbert spaces, another generalization of finite-dimensional Euclidean spaces. They were introduced...

uses mainly a part of functional analysis, especially Hilbert spaces, which are a kind of linear space. Such are distinguished from mathematical formalisms...

length k ≤ n. This upper bound on the projective dimension is sharp, that is, there are modules of projective dimension exactly n. The standard example...

holomorphic Complex projective space, a projective space with respect to the field of complex numbers Unitary space, a vector space with the addition of...

Segre embedding is used in projective geometry to consider the cartesian product (of sets) of two projective spaces as a projective variety. It is named after...