In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the following: If U is an open subset of Rn and f: U → Rm is Lipschitz...

In mathematical analysis, the Rademacher–Menchov theorem, introduced by Rademacher (1922) and Menchoff (1923), gives a sufficient condition for a series...

transform Rademacher's contour Rademacher complexity Rademacher function Rademacher–Menchov theorem Rademacher's series Rademacher system Rademacher distribution...

Lipschitz continuous with Lipschitz constant at most K. More generally, Rademacher's theorem extends the differentiability result to Lipschitz mappings between...

and whose inverse function φ−1 : φ(U) → U is also Lipschitz. By Rademacher's theorem, a bi-Lipschitz mapping is differentiable almost everywhere. In particular...

(functional analysis) Rademacher's theorem (mathematical analysis) Rising sun lemma (real analysis) Rolle's theorem (calculus) Squeeze theorem (mathematical analysis)...

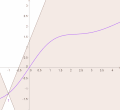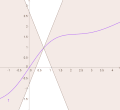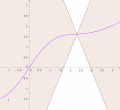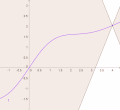
set of non-differentiability points must be a Lebesgue null set (Rademacher's theorem). When we try to draw a general continuous function, we usually draw...

error smaller than any quadratic. The result is closely related to Rademacher's theorem. Niculescu, Constantin P.; Persson, Lars-Erik (2005). Convex Functions...

system of functions Rademacher's theorem, a statistical theorem in measure theory This page lists people with the surname Rademacher. If an internal link...

derivative, one can generalize Rademacher's theorem to metric space-valued Lipschitz functions. Rademacher's theorem states that a Lipschitz map f : Rn → Rm...

{2}{3}}\left(n-{\frac {1}{24}}\right)}}}\,\,\,\right]}\right).} The proof of Rademacher's formula involves Ford circles, Farey sequences, modular symmetry and...

Giorgio Gnecco, Marcello Sanguineti (2008) Approximation Error Bounds via Rademacher's Complexity. Applied Mathematical Sciences, Vol. 2, 2008, no. 4, 153–176...

In probability theory and statistics, the Rademacher distribution (which is named after Hans Rademacher) is a discrete probability distribution where...

Rademacher, Hans; Toeplitz, Otto (1990). The Enjoyment of Mathematics. Dover. chapter 16. ISBN 978-0-486-26242-0. Weisstein, Eric W. "Jung's Theorem"...

In number theory, the von Staudt–Clausen theorem is a result determining the fractional part of Bernoulli numbers, found independently by Karl von Staudt (1840)...

The fluctuation theorem (FT), which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently...

In mathematics, Midy's theorem, named after French mathematician E. Midy, is a statement about the decimal expansion of fractions a/p where p is a prime...

In mathematics, the Brunn–Minkowski theorem (or Brunn–Minkowski inequality) is an inequality relating the volumes (or more generally Lebesgue measures)...

ISBN 0-387-97127-0. Zbl 0697.10023. (See chapter 5 for a modern pedagogical intro to Rademacher's formula). Bóna, Miklós (2002). A Walk Through Combinatorics: An Introduction...

number on the upper half-plane, but i is the most convenient choice.) Rademacher's contour is (more or less) given by the boundaries of all the Ford circles...

pseudoconex A pseudoconvex set is a generalization of a convex set. Rademacher Rademacher's theorem says a locally Lipschitz function is differentiable almost...

that this limit exists. A key theorem in this area is the Pansu–Rademacher theorem, a generalization of Rademacher's theorem, which can be stated as follows:...

encodes the lengths and area. Reciprocally, according to the Nash-Kuiper theorem, any Riemannian surface with boundary can be embedded in Euclidean space...

claim. The Jacobian is defined almost everywhere by Rademacher's differentiability theorem. The theorem was proved first by Herbert Federer (Federer 1969)...

differential calculus for Lipschitz continuous functions, which uses Rademacher's theorem and which is described by Rockafellar & Wets (1998) and Mordukhovich...

experiments with biomolecules to numerical simulations. The Crooks fluctuation theorem, proved two years later, leads immediately to the Jarzynski equality. Many...

powers. Hans Rademacher and Otto Toeplitz, The Enjoyment of Mathematics (1933) (ISBN 0-691-02351-4). Has a proof of the Lagrange theorem, accessible to...

Kirchberger's theorem is a theorem in discrete geometry, on linear separability. The two-dimensional version of the theorem states that, if a finite set...

all f ∈ F {\displaystyle f\in {\mathcal {F}}} . uniform central limit theorem: G n = n ( P n − P ) ⇝ G , in  ℓ ∞ ( F ) {\displaystyle \mathbb {G} _{n}={\sqrt...

Cramér had published an almost identical concept now known as Cramér's theorem. It is a sharper bound than the first- or second-moment-based tail bounds...