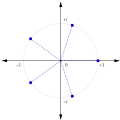
number theory, a kth root of unity modulo n for positive integers k, n ≥ 2, is a root of unity in the ring of integers modulo n; that is, a solution x...

a primitive root modulo n if every number a coprime to n is congruent to a power of g modulo n. That is, g is a primitive root modulo n if for every...

of modular integers, see Root of unity modulo n. Every nth root of unity z is a primitive ath root of unity for some a ≤ n, which is the smallest positive...

mathematics, a primitive root may mean: Primitive root modulo n in modular arithmetic Primitive nth root of unity amongst the solutions of zn = 1 in a field...

n/2-th root of −1 is a principal n-th root of unity. A non-example is 3 {\displaystyle 3} in the ring of integers modulo 26 {\displaystyle 26} ; while 3...

n {\displaystyle n} th primitive root of unity if and only if n {\displaystyle n} is a divisor of q − 1 {\displaystyle q-1} ; if n {\displaystyle n}...

above. Apotome (mathematics) Cube root Functional square root Integer square root Nested radical Nth root Root of unity Solving quadratic equations with...

polynomial has a simple root modulo a prime number p, then this root can be lifted to a unique root modulo any higher power of p. More generally, if a...

the field of the rational numbers of any primitive nth-root of unity ( e 2 i π / n {\displaystyle e^{2i\pi /n}} is an example of such a root). An important...

congruence classes (mod n) represented by integers coprime to n. They constitute the multiplicative group of integers modulo n. In the ring Z[√3] obtained...

principal nth root of unity, defined by: The discrete Fourier transform maps an n-tuple ( v 0 , … , v n − 1 ) {\displaystyle (v_{0},\ldots ,v_{n-1})} of elements...

{\displaystyle G(a,\chi )=\sum _{n=0}^{p-1}\chi (n)\,\zeta _{p}^{an}} is the Gauss sum defined for any character χ modulo p. The value of the Gauss sum is an algebraic...

integers. Every finite cyclic group of order n is isomorphic to the additive group of Z/nZ, the integers modulo n. Every cyclic group is an abelian group...

n ′ + 1 ) {\displaystyle g^{D/2}\equiv -1{\pmod {2^{n'}+1}}} , and so g {\displaystyle g} is a primitive D {\displaystyle D} th root of unity modulo 2...

algorithms depend only on the fact that e − 2 π i / n {\textstyle e^{-2\pi i/n}} is an nth primitive root of unity, and thus can be applied to analogous transforms...

contains n distinct nth roots of unity, which implies that the characteristic of K doesn't divide n, then adjoining to K the nth root of any element a of K creates...

element of Z[ζ] that is coprime to a and l {\displaystyle l} and congruent to a rational integer modulo (1–ζ)2. Suppose that ζ is an lth root of unity for...

th root of unity, with p {\displaystyle p} an odd prime number. The uniqueness is a consequence of Galois theory, there being a unique subgroup of index...

the seventeenth root of unity ζ = exp ⁡ ( 2 π i 17 ) . {\displaystyle \zeta =\exp \left({\frac {2\pi i}{17}}\right).} Given an integer n > 1, let H be any...

context of the above material, what these latter authors have achieved is to find N much less than 23k + 1, so that Z/NZ has a (2m)th root of unity. This...

has a root in F. In other words, a field is algebraically closed if the fundamental theorem of algebra holds for it. For example, the field of real numbers...

group of (pr − 1)-th roots of unity. It is a cyclic group of order pr − 1. The subgroup G2 is 1+pR, consisting of all elements congruent to 1 modulo p. It...

m^{2}+1} : or in other words, a 'square root of -1 modulo p {\displaystyle p} ' . We claim such a square root of − 1 {\displaystyle -1} is given by K =...

\dots ,u_{r}} are a set of generators for the unit group of K modulo roots of unity. There will be r + 1 Archimedean places of K, either real or complex...

{-1+i{\sqrt {3}}}{2}}=e^{i2\pi /3}} is a primitive (hence non-real) cube root of unity. The Eisenstein integers form a triangular lattice in the complex plane...

Q and p(x) = x3 − 2. Each root of p equals 3√2 times a cube root of unity. Therefore, if we denote the cube roots of unity by ω 1 = 1 , {\displaystyle...

the law of quadratic reciprocity is a theorem about modular arithmetic that gives conditions for the solvability of quadratic equations modulo prime numbers...

the entire field GF(pm). This implies that α is a primitive (pm − 1)-root of unity in GF(pm). Because all minimal polynomials are irreducible, all primitive...

rational root theorem, this has no rational zeroes. Neither does it have linear factors modulo 2 or 3. The Galois group of f(x) modulo 2 is cyclic of order...

by adjoining a primitive n-th root of unity ζ n {\displaystyle \zeta _{n}} . This field contains all complex nth roots of unity and its dimension over Q...