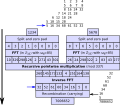
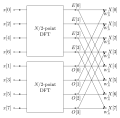
Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers, published by Arnold Schönhage and Volker Strassen...

Strassen (1968). It was made practical and theoretical guarantees were provided in 1971 by Schönhage and Strassen resulting in the Schönhage–Strassen...

in Tübingen and Konstanz. Together with Volker Strassen, he developed the Schönhage–Strassen algorithm for the multiplication of large numbers that has...

"grade school" algorithm. The Toom–Cook algorithm (1963) is a faster generalization of Karatsuba's method, and the Schönhage–Strassen algorithm (1971) is even...

asymptotically faster Schönhage–Strassen algorithm (with complexity Θ(n log n log log n)) becomes practical. Toom first described this algorithm in 1963, and Cook...

numbers Karatsuba algorithm Schönhage–Strassen algorithm Toom–Cook multiplication Odlyzko–Schönhage algorithm: calculates nontrivial zeroes of the Riemann...

the binary GCD algorithm using ideas from the Schönhage–Strassen algorithm for fast integer multiplication. The binary GCD algorithm has also been extended...

transform; see the Schönhage–Strassen algorithm. Strassen is also known for his 1977 work with Robert M. Solovay on the Solovay–Strassen primality test,...

Odlyzko–Schönhage algorithm applies the FFT to finite Dirichlet series Schönhage–Strassen algorithm – asymptotically fast multiplication algorithm for large...

series, showing that it is also O(h2). Modern algorithmic techniques based on the Schönhage–Strassen algorithm for fast integer multiplication can be used...

discarding portions of the output. Other fast convolution algorithms, such as the Schönhage–Strassen algorithm or the Mersenne transform, use fast Fourier transforms...

The Solovay–Strassen primality test, developed by Robert M. Solovay and Volker Strassen in 1977, is a probabilistic primality test to determine if a number...

efficient multiplication algorithm such as the Karatsuba algorithm, Toom–Cook multiplication or the Schönhage–Strassen algorithm. The result is that the...

and computer programming, the extended Euclidean algorithm is an extension to the Euclidean algorithm, and computes, in addition to the greatest common...

test: an algorithm which determines whether a given number is likely to be prime, similar to the Fermat primality test and the Solovay–Strassen primality...

subsequent discovery of the Solovay–Strassen and Miller–Rabin algorithms put PRIMES in coRP. In 1992, the Adleman–Huang algorithm reduced the complexity to ⁠...

has b = O ( n log ⁡ n ) {\displaystyle b=O(n\log n)} bits. The Schönhage–Strassen algorithm can produce a b {\displaystyle b} -bit product in time O ( b...

In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking...

Multiplication algorithm Karatsuba algorithm, for large numbers Toom–Cook multiplication, for very large numbers Schönhage–Strassen algorithm, for huge numbers...

straightforward "schoolbook algorithm". The first to be discovered was Strassen's algorithm, devised by Volker Strassen in 1969 and often referred to...

{\displaystyle \mathbb {Z} } . Fürer's algorithm Karatsuba algorithm Mixed-precision arithmetic Schönhage–Strassen algorithm Toom–Cook multiplication Little...

The Tonelli–Shanks algorithm (referred to by Shanks as the RESSOL algorithm) is used in modular arithmetic to solve for r in a congruence of the form r2...

Shor's algorithm is a quantum algorithm for finding the prime factors of an integer. It was developed in 1994 by the American mathematician Peter Shor...

Pollard's rho algorithm is an algorithm for integer factorization. It was invented by John Pollard in 1975. It uses only a small amount of space, and...

In computational number theory, Cipolla's algorithm is a technique for solving a congruence of the form x 2 ≡ n ( mod p ) , {\displaystyle x^{2}\equiv...

complexity is O(p3). A more efficient multiplication algorithm is the Schönhage–Strassen algorithm, which is based on the Fast Fourier transform. It only...

theory, Williams's p + 1 algorithm is an integer factorization algorithm, one of the family of algebraic-group factorisation algorithms. It was invented by...

multiplication techniques such as Toom–Cook multiplication and the Schönhage–Strassen algorithm must be used; with ordinary O(n2) multiplication, binary splitting...

Pollard's rho algorithm for logarithms is an algorithm introduced by John Pollard in 1978 to solve the discrete logarithm problem, analogous to Pollard's...

y {\displaystyle y} and k {\displaystyle k} be non-negative integers. Algorithms that compute (the decimal representation of) y {\displaystyle {\sqrt {y}}}...