Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Although objects of any...

In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in...

In set theory, the complement of a set A, often denoted by A c {\displaystyle A^{c}} (or A′), is the set of elements not in A. When all elements in the...

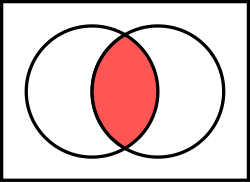
In set theory, the intersection of two sets A {\displaystyle A} and B , {\displaystyle B,} denoted by A ∩ B , {\displaystyle A\cap B,} is the set containing...

In set theory and its applications throughout mathematics, a class is a collection of sets (or sometimes other mathematical objects) that can be unambiguously...

Appendix:Glossary of set theory in Wiktionary, the free dictionary. This is a glossary of terms and definitions related to the topic of set theory. Contents: ...

Axiomatic constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. The same first-order language...

In set theory, the union (denoted by ∪) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations...

Musical set theory provides concepts for categorizing musical objects and describing their relationships. Howard Hanson first elaborated many of the concepts...

Look up set theory in Wiktionary, the free dictionary. Set theory is a branch of mathematics concerning mathematical sets. A set theory may also refer...

Naive set theory is any of several theories of sets used in the discussion of the foundations of mathematics. Unlike axiomatic set theories, which are...

example being the neighborhood filter. Filters appear in order theory, model theory, and set theory, but can also be found in topology, from which they originate...

Neumann–Bernays–Gödel set theory (NBG) is an axiomatic set theory that is a conservative extension of Zermelo–Fraenkel–choice set theory (ZFC). NBG introduces...

In mathematical logic, descriptive set theory (DST) is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...

Quasi-set theory is a formal mathematical theory for dealing with collections of objects, some of which may be indistinguishable from one another. Quasi-set...

contradictions within modern axiomatic set theory. Set theory as conceived by Georg Cantor assumes the existence of infinite sets. As this assumption cannot be...

In the mathematical field of set theory, the continuum means the real numbers, or the corresponding (infinite) cardinal number, denoted by c {\displaystyle...

graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set S...

conditions for a topological space to be metrizable. Set-theoretic topology is a subject that combines set theory and general topology. It focuses on topological...

Internal set theory Pocket set theory Naive set theory S (set theory) Double extension set theory Kripke–Platek set theory Kripke–Platek set theory with urelements...

set theory (sometimes denoted by Z-), as set out in a seminal paper in 1908 by Ernst Zermelo, is the ancestor of modern Zermelo–Fraenkel set theory (ZF)...

In mathematical set theory, the multiverse view is that there are many models of set theory, but no "absolute", "canonical" or "true" model. The various...

"Set Theory", Stanford Encyclopedia of Philosophy, Metaphysics Research Lab, Stanford University Suppes, Patrick (1972) [1960], Axiomatic Set Theory,...

Non-well-founded set theories are variants of axiomatic set theory that allow sets to be elements of themselves and otherwise violate the rule of well-foundedness...

Major subareas include model theory, proof theory, set theory, and recursion theory (also known as computability theory). Research in mathematical logic...

empty set or void set is the unique set having no elements; its size or cardinality (count of elements in a set) is zero. Some axiomatic set theories ensure...

Kripke–Platek set theory (KP), pronounced /ˈkrɪpki ˈplɑːtɛk/, is an axiomatic set theory developed by Saul Kripke and Richard Platek. The theory can be thought...

in set theory, the constructible universe (or Gödel's constructible universe), denoted by L , {\displaystyle L,} is a particular class of sets that...

to sets see the article on sets, for a fuller account see naive set theory, and for a full rigorous axiomatic treatment see axiomatic set theory. The...

mathematics, the power set (or powerset) of a set S is the set of all subsets of S, including the empty set and S itself. In axiomatic set theory (as developed...