Sparse matrix–vector multiplication (SpMV) of the form y = Ax is a widely used computational kernel existing in many scientific applications. The input...

Leiserson, Charles E. (2009). Parallel sparse matrix-vector and matrix-transpose-vector multiplication using compressed sparse blocks (PDF). ACM Symp. on Parallelism...

Because matrix multiplication is such a central operation in many numerical algorithms, much work has been invested in making matrix multiplication algorithms...

5\end{smallmatrix}}\right]} . In geometry, a diagonal matrix may be used as a scaling matrix, since matrix multiplication with it results in changing scale (size)...

complexity of matrix multiplication dictates how quickly the operation of matrix multiplication can be performed. Matrix multiplication algorithms are a central...

perform the matrix–vector and transpose matrix–vector multiplications. Therefore, CGNR is particularly useful when A is a sparse matrix since these operations...

a vector space. Specifically, when the vector space comprises matrices, such norms are referred to as matrix norms. Matrix norms differ from vector norms...

the matrix multiplication A v = λ v , {\displaystyle A\mathbf {v} =\lambda \mathbf {v} ,} where the eigenvector v is an n by 1 matrix. For a matrix, eigenvalues...

edges between two vertices P system – Computational model Sparse matrix–vector multiplication – Computation routine Petri Net – Model to describe distributed...

algebra operations such as vector addition, scalar multiplication, dot products, linear combinations, and matrix multiplication. They are the de facto standard...

be expressed as multiplication of a two-component vector with a two-by-two matrix called ray transfer matrix analysis: the vector's components are the...

n} matrix, it is a property of matrix multiplication that I m A = A I n = A . {\displaystyle I_{m}A=AI_{n}=A.} In particular, the identity matrix serves...

the complex numbers, but since complex multiplication can be implemented as real 2-by-2 matrix multiplication, this is a mere notational difference. Like...

eliminate this loss of orthogonality. NIPALS reliance on single-vector multiplications cannot take advantage of high-level BLAS and results in slow convergence...

severally, with respect to the scalar argument in scalar–vector multiplication and with respect to its vector argument. Abusing terminology, some engineers[who...

gains by using MPI-IO. For example, an implementation of sparse matrix-vector multiplications using the MPI I/O library shows a general behavior of minor...

hierarchical matrices (H-matrices) are used as data-sparse approximations of non-sparse matrices. While a sparse matrix of dimension n {\displaystyle n} can be represented...

derived from the spectral theorem. A (nonzero) vector v of dimension N is an eigenvector of a square N × N matrix A if it satisfies a linear equation of the...

include: fast large-integer multiplication algorithms and polynomial multiplication, efficient matrix–vector multiplication for Toeplitz, circulant and...

When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases: b n...

non-negative matrix factorization has a long history under the name "self modeling curve resolution". In this framework the vectors in the right matrix are continuous...

Triangular matrix Tridiagonal matrix Block matrix Sparse matrix Hessenberg matrix Hessian matrix Vandermonde matrix Stochastic matrix Toeplitz matrix Circulant...

Charles E. (2009), "Parallel sparse matrix-vector and matrix-transpose-vector multiplication using compressed sparse blocks", ACM Symp. on Parallelism...

the algorithm is the multiplication of matrix A {\displaystyle A} by a vector, so it is effective for a very large sparse matrix with appropriate implementation...

units. The scan operation has uses in e.g., quicksort and sparse matrix-vector multiplication. The scatter operation is most naturally defined on the vertex...

block matrix. It is a specialization of the tensor product (which is denoted by the same symbol) from vectors to matrices and gives the matrix of the...

Georgios; Koziris, Nectarios (2008-01-01). "Optimizing sparse matrix-vector multiplication using index and value compression". Proceedings of the 5th...

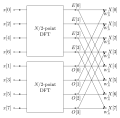
finite-dimensional vector space, the DFT expression can also be written in terms of a DFT matrix; when scaled appropriately it becomes a unitary matrix and the Xk...

the zero matrix. Identity matrix, the multiplicative identity for matrices Matrix of ones, a matrix where all elements are one Nilpotent matrix Single-entry...

strided: Sparse matrix-vector multiplication. Sparse matrix-dense matrix multiplication. Sparse matrix-vector triangular solve. Sparse matrix-dense matrix triangular...