In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical...

In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement (or lattice). Carl Friedrich...

A sphere (from Greek σφαῖρα, sphaîra) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the...

⁠ O P 1 {\displaystyle \mathbf {OP} ^{1}} ⁠. 23-sphere A highly dense sphere-packing is possible in ⁠ 24 {\displaystyle 24} ⁠-dimensional space, which...

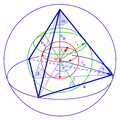
Sphere packing in a sphere is a three-dimensional packing problem with the objective of packing a given number of equal spheres inside a unit sphere. It...

Sphere packing in a cylinder is a three-dimensional packing problem with the objective of packing a given number of identical spheres inside a cylinder...

Circumscribed sphere Inscribed circle Midsphere Sphere packing Coxeter, H.S.M. Regular Polytopes 3rd Edn. Dover (1973). Cundy, H.M. and Rollett, A.P. Mathematical...

Apollonian sphere packing is the three-dimensional equivalent of the Apollonian gasket. The principle of construction is very similar: with any four spheres that...

arranged in that space such that they each touch a common unit sphere. For a given sphere packing (arrangement of spheres) in a given space, a kissing...

In mathematics, the theory of finite sphere packing concerns the question of how a finite number of equally-sized spheres can be most efficiently packed...

In geometry, sphere packing in a cube is a three-dimensional sphere packing problem with the objective of packing spheres inside a cube. It is the three-dimensional...

this is called sphere packing, which usually deals only with identical spheres. The branch of mathematics generally known as "circle packing" is concerned...

spheres are widely used as model particles in the statistical mechanical theory of fluids and solids. They are defined simply as impenetrable spheres...

code: it is also known as the sphere-packing bound or the volume bound from an interpretation in terms of packing balls in the Hamming metric into the space...

1-skeleton of a simplicial complex which is homeomorphic to the sphere. The circle packing theorem guarantees the existence of a circle packing with finitely...

Unsolved problem in mathematics Is there any three-dimensional convex body with lower packing density than the sphere? More unsolved problems in mathematics...

offer the best lattice packing of spheres, and is believed to be the optimal of all packings. With 'simple' sphere packings in three dimensions ('simple'...

Kepler, is a mathematical theorem about sphere packing in three-dimensional Euclidean space. It states that no arrangement of equally sized spheres filling...

University Press. ISBN 052120125X. Boerdijk, A.H. (1952). "Some remarks concerning close-packing of equal spheres". Philips Res. Rep. 7: 303–313. Fuller, R...

packing in a circle Sphere packing in a cube Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1991). Unsolved Problems in Geometry. New York:...

In crystallography, atomic packing factor (APF), packing efficiency, or packing fraction is the fraction of volume in a crystal structure that is occupied...

n-dimensional spheres of a fixed radius in Rn so that no two spheres overlap. Lattice packings are special types of sphere packings where the spheres are centered...

wʲɐˈzɔu̯sʲkɐ]; born 2 December 1984) is a Ukrainian mathematician known for her work in sphere packing. She is a full professor and Chair of Number Theory...

1939) is a British-American mathematician. His major contributions are in the fields of combinatorics, error-correcting codes, and sphere packing. Sloane...

out in a celebrated list compiled in 1900 by mathematician David Hilbert. It asks three separate questions about lattices and sphere packing in Euclidean...

angles between pairs of circles in a circle packing whose corresponding polyhedron has the desired relation to its sphere. In any dimension higher than three...

In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every edge of the polyhedron. Not every polyhedron has...

the packing of four equal spheres. The dense random packing of hard spheres problem can thus be mapped on the tetrahedral packing problem. It is a practical...

Random close packing (RCP) of spheres is an empirical parameter used to characterize the maximum volume fraction of solid objects obtained when they are...

A packing density or packing fraction of a packing in some space is the fraction of the space filled by the figures making up the packing. In simplest...