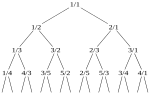
In number theory, the Stern–Brocot tree is an infinite complete binary tree in which the vertices correspond one-for-one to the positive rational numbers...

infinite binary search tree, called the Stern–Brocot tree. The number 1 (expressed as a fraction 1/1) is placed at the root of the tree, and the location of...

Moritz Abraham Stern, a 19th-century German mathematician who also invented the closely related Stern–Brocot tree. Even earlier, a similar tree (including...

series". Cut-the-Knot. Bogomolny, Alexander. "Stern-Brocot Tree". Cut-the-Knot. Pennestri, Ettore. "A Brocot table of base 120". "Farey series", Encyclopedia...

with, but independently of, German number theorist Moritz Stern) of the Stern–Brocot tree, a mathematical structure useful in approximating real numbers...

Farey sequences Fn are successively built up with increasing n. The Stern–Brocot tree provides an enumeration of all positive rational numbers via mediants...

{R} } is defined via the codenominator. Jimm relates the Stern-Brocot tree to the Bird tree. Jimm induces an involution of the moduli space of rank-2...

more than twice. He is also known for the Stern–Brocot tree, which he wrote about in 1858 and which Brocot independently discovered in 1861. Setting the...

as can be seen by a recursive definition closely related to the Stern–Brocot tree. One way to define the question-mark function involves the correspondence...

of a given unit m. This problem is related to Farey sequences, the Stern–Brocot tree, and continued fractions. Finished lumber, writing paper, electronic...

or the next smaller ancestor to p / q {\displaystyle p/q} in the Stern–Brocot tree or where p / q {\displaystyle p/q} is the next larger or next smaller...

matrix product and integration over a certain fractal measure on the Stern–Brocot tree. Moreover, Viswanath computed the numerical value above using floating...

where L and R are the standard left and right moves on the Stern–Brocot tree; it is well known that these moves generate the modular group. Alternately...

fraction Recurring decimal Cyclic number Farey sequence Ford circle Stern–Brocot tree Dedekind sum Egyptian fraction Montgomery reduction Modular exponentiation...

representation Restricted partial quotients – Analytic series Stern–Brocot tree – Ordered binary tree of rational numbers Pettofrezzo & Byrkit 1970, p. 150....

17 (4): 333–339. MR 0550175. Gibbs, Philip (1999). "A Generalised Stern-Brocot Tree from Regular Diophantine Quadruples". arXiv:math.NT/9903035v1. Herrmann...

development—without the use of continued fractions—of the theory of the Stern–Brocot tree, which codifies the new rational endpoints that appear at the nth...