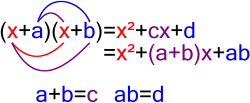mathematics, a surjective function (also known as surjection, or onto function /ˈɒn.tuː/) is a function f such that, for every element y of the function's codomain...
17 KB (1,948 words) - 14:12, 3 July 2025
Bijection, injection and surjection (category Functions and mappings)
domain; that is, if the image and the codomain of the function are equal. A surjective function is a surjection. Notationally: ∀ y ∈ Y , ∃ x ∈ X , y =...
15 KB (2,207 words) - 15:52, 23 October 2024
of a function are the same set; such a function is called surjective or onto. For any non-surjective function f : X → Y , {\displaystyle f:X\to Y,} the...
6 KB (830 words) - 20:35, 6 June 2025
Bijection (redirect from Bijective function)
element of Y. Functions which satisfy property (3) are said to be "onto Y " and are called surjections (or surjective functions). Functions which satisfy...
19 KB (2,508 words) - 09:01, 28 May 2025
injective non-surjective function (injection, not a bijection) An injective surjective function (bijection) A non-injective surjective function (surjection...
17 KB (2,589 words) - 07:48, 3 July 2025
analogues of onto or surjective functions (and in the category of sets the concept corresponds exactly to the surjective functions), but they may not exactly...
18 KB (2,481 words) - 19:57, 5 July 2025
{\displaystyle y\in Y} implies that f is surjective. The inverse function f −1 to f can be explicitly described as the function f − 1 ( y ) = ( the unique element ...
43 KB (5,224 words) - 09:30, 6 June 2025
set X is equivalent to counting injective functions N → X when n = x, and also to counting surjective functions N → X when n = x. Counting multisets of...
43 KB (5,609 words) - 19:20, 19 January 2025
composition of one-to-one (injective) functions is always one-to-one. Similarly, the composition of onto (surjective) functions is always onto. It follows that...
37 KB (3,772 words) - 08:50, 25 February 2025
injective function from S {\displaystyle S} to N {\displaystyle \mathbb {N} } . S {\displaystyle S} is empty or there exists a surjective function from N...
28 KB (4,381 words) - 01:01, 29 March 2025
thus f − 1 ( y ) = { x } . {\displaystyle f^{-1}(y)=\{x\}.} The function f is surjective (or onto, or is a surjection) if its range f ( X ) {\displaystyle...
76 KB (11,410 words) - 20:15, 22 May 2025
element x in the domain X. The identity function on X is clearly an injective function as well as a surjective function (its codomain is also its range), so...
6 KB (629 words) - 16:15, 2 July 2025
well-order. Since the collection of all ordinals such that there exists a surjective function from B {\displaystyle B} to the ordinal is a set, there exists an...
4 KB (583 words) - 22:20, 18 October 2023
partial functions. A partial function is said to be injective, surjective, or bijective when the function given by the restriction of the partial function to...
15 KB (2,055 words) - 16:59, 20 May 2025
13 function is an example of a simple-to-define function which takes on every real value in every interval, that is, it is an everywhere surjective function...
8 KB (1,228 words) - 12:43, 28 June 2025
example, to say that a function is onto (surjective) or not the codomain should be taken into account. The graph of a function on its own does not determine...
7 KB (961 words) - 07:13, 5 March 2025
Pathological (mathematics) (redirect from Pathological function)
Riemann-integrable. The Peano space-filling curve is a continuous surjective function that maps the unit interval [ 0 , 1 ] {\displaystyle [0,1]} onto...
19 KB (2,392 words) - 23:47, 19 June 2025
this equivalence. Any injective function between two finite sets of the same cardinality is also a surjective function (a surjection). Similarly, any surjection...
18 KB (2,594 words) - 16:45, 4 July 2025
{\displaystyle K/k} . A discrete valuation of K / k {\displaystyle K/k} is a surjective function v : K → Z ∪ { ∞ } {\displaystyle v:K\to \mathbb {Z} \cup \{\infty...
7 KB (1,154 words) - 23:58, 25 June 2025
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept...
19 KB (2,475 words) - 06:23, 2 July 2025
In category theory, a point-surjective morphism is a morphism f : X → Y {\displaystyle f:X\rightarrow Y} that "behaves" like surjections on the category...
5 KB (758 words) - 19:11, 5 June 2025
rank function. Thus the constant rank theorem applies to a generic point of the domain. When the derivative of F is injective (resp. surjective) at a...
42 KB (7,935 words) - 05:47, 16 July 2025
elements of a set J, then J is an index set. The indexing consists of a surjective function from J onto A, and the indexed collection is typically called an...
2 KB (298 words) - 06:46, 10 May 2024
of X not included in it. That is, X is nonempty and there is no surjective function from the natural numbers to X. The cardinality of X is neither finite...
6 KB (884 words) - 06:49, 8 April 2025
one-to-one function. In other words, every element of the function's codomain is the image of at most one element of its domain. Surjective function: has a...
13 KB (1,407 words) - 00:18, 19 May 2025
Tuple (section Tuples as functions)
{\displaystyle \left(a_{1},\ldots ,a_{n}\right)} may be identified with the (surjective) function F : { 1 , … , n } → { a 1 , … , a n } {\displaystyle F~:~\left\{1...
16 KB (2,224 words) - 06:56, 3 May 2025
cardinality of S is less than the cardinality of T, then there is no surjective function from S to T. Let q1, q2, ..., qn be positive integers. If q 1 + q...
31 KB (4,190 words) - 00:29, 5 July 2025
of surjective functions f {\displaystyle f} and g {\displaystyle g} also implies the existence of a bijection. We construct an injective function h :...
20 KB (2,374 words) - 11:57, 23 March 2025
objects. For example, every function may be factored into the composition of a surjective function with an injective function. Matrices possess many kinds...
42 KB (7,863 words) - 13:39, 5 June 2025
characteristic function of a subset A of some set X maps elements of X to the codomain { 0 , 1 } . {\displaystyle \{0,\,1\}.} This mapping is surjective only when...
17 KB (2,543 words) - 13:47, 8 May 2025