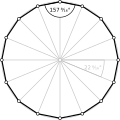
In mathematics, Viète's formula is the following infinite product of nested radicals representing twice the reciprocal of the mathematical constant π:...

mathematics, Vieta's formulas relate the coefficients of a polynomial to sums and products of its roots. They are named after François Viète (1540-1603), more...

Pascal all used Viète's symbolism. About 1770, the Italian mathematician Targioni Tozzetti, found in Florence Viète's Harmonicon coeleste. Viète had written...

obtained from polygons with fewer sides. Viète's formula, published by François Viète in 1593, was derived by Viète using a closely related polygonal method...

written using binomial coefficients. This formula was given by 16th century French mathematician François Viète: sin ⁡ n x = ∑ k = 0 n ( n k ) ( cos ⁡ x...

infinitesimal calculus and pi. Viète's formula, a different infinite product formula for π {\displaystyle \pi } . Leibniz formula for π, an infinite sum that...

estimate π to 11 digits around 1400. In 1593, François Viète published what is now known as Viète's formula, an infinite product (rather than an infinite sum...

formulae for π, such as the following two products, respectively by Viète (Viète's formula, the first published infinite product in mathematics) and John Wallis...

{1}{3}}\right)^{+1}\cdots } (another form of Wallis product) Viète's formula: 2 π = 2 2 ⋅ 2 + 2 2 ⋅ 2 + 2 + 2 2 ⋅ ⋯ {\displaystyle {\frac {2}{\pi...

the quadratic formula in the form we know today. Vieta's formulas (named after François Viète) are the relations x 1 + x 2 = − b a , x 1 x 2 = c a {\displaystyle...

{2+\dots +{\sqrt {2}}}}}}}} _{n}=\pi } . This can be derived from Viète's formula for π. Asymptotic equivalences, f ( x ) ∼ g ( x ) {\displaystyle f(x)\sim...

area can be computed in terms of the circumradius R by truncating Viète's formula: A = R 2 ⋅ 2 1 ⋅ 2 2 ⋅ 2 2 + 2 = 4 R 2 2 − 2 . {\displaystyle A=R^{2}\cdot...

-coefficient of Δ {\displaystyle \Delta } is the Ramanujan tau function. Viète's formula for π can be written: 2 π = 1 2 ⋅ 1 2 + 1 2 1 2 ⋅ 1 2 + 1 2 1 2 + 1...

pattern of the signs is ( + , + , − , + ) . {\displaystyle (+,+,-,+).} Viète's formula for π, the ratio of a circle's circumference to its diameter, is 2...

mathematicians, cannot be solved by compass-and-straightedge construction. Viète's trigonometric expression of the roots in the three-real-roots case lends...

} the following is true, and can be deduced using De Moivre's formula, Euler's formula and the binomial theorem. The product-to-sum identities or prosthaphaeresis...

Ramanujan–Sato series Rhind Mathematical Papyrus Salamin–Brent algorithm Software for calculating π Squaring the circle Turn (geometry) Viète's formula...

^{~\cdot ^{~\cdot }}}}}=2.} 2 {\displaystyle {\sqrt {2}}} appears in Viète's formula for π, 2 π = 1 2 ⋅ 1 2 + 1 2 1 2 ⋅ 1 2 + 1 2 1 2 + 1 2 1 2 ⋯ , {\displaystyle...

claims that François Viète used the trisectrix to derive Viète's formula, an infinite product of nested radicals published by Viète in 1593 that converges...

In mathematics, the Leibniz formula for π, named after Gottfried Wilhelm Leibniz, states that π 4 = 1 − 1 3 + 1 5 − 1 7 + 1 9 − ⋯ = ∑ k = 0 ∞ ( − 1 )...

term). 16th century: François Viète discovers Vieta's formulas. 16th century: François Viète discovers Viète's formula for π.1500: Scipione del Ferro...

)}},} which is equivalent to the generalization of Morrie's law. Viète's formula, same identity taking α = 2 − n x {\displaystyle \alpha =2^{-n}x} on...

functions have analogues involving the lemniscate functions. For example, Viète's formula for π can be written: 2 π = 1 2 ⋅ 1 2 + 1 2 1 2 ⋅ 1 2 + 1 2 1 2 + 1...

In trigonometry, tangent half-angle formulas relate the tangent of half of an angle to trigonometric functions of the entire angle. The tangent of half...

that is, only working on the coefficients of the polynomial. Finally, Viète's formulas are used in order to approximate the roots. Let p(x) be a polynomial...

formalized by the 16th-century French mathematician François Viète, in Viète's formulas, for the case of positive real roots. In the opinion of the 18th-century...

Leibniz formula for π — alternating series with very slow convergence Wallis product — infinite product converging slowly to π/2 Viète's formula — more...

and coefficients of quadratic and cubic equations, which is called "Viete's formulas" now. Trigonometry also achieved greater development during the Renaissance...

the roots. This greatly magnifies variances in the roots. Applying Viète's formulas, one obtains easy approximations for the modulus of the roots, and...

and early 17th century for approximate multiplication and division using formulas from trigonometry. For the 25 years preceding the invention of the logarithm...