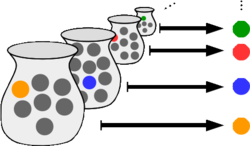
and in particular measure theory, a measurable function is a function between the underlying sets of two measurable spaces that preserves the structure...

analysis—a weakly measurable function taking values in a Banach space is a function whose composition with any element of the dual space is a measurable function...

Bochner-measurable function taking values in a Banach space is a function that equals almost everywhere the limit of a sequence of measurable countably-valued...

(they are in fact weakly Mahlo). All measurable cardinals are real-valued measurable, and a real-valued measurable cardinal κ is measurable if and only if...

measurable selection theorem is a result from measure theory that gives a sufficient condition for a set-valued function to have a measurable selection...

lifting to a ‘weakly’ measurable function with values in a weakly compact set of a Banach space, one obtains a strongly measurable function; this gives...

{\displaystyle \{s\in S:f(s)\neq g(s)\}} is measurable and has measure zero. Similarly, a measurable function f {\displaystyle f} (and its absolute value)...

Lebesgue-measurable functions does not have to be Lebesgue-measurable as well. Nevertheless, a composition of a measurable function with a continuous function...

≤ p ≤ ∞ {\displaystyle 1\leq p\leq \infty } , is the Lp space of measurable functions whose p-norm ‖ f ‖ p = ( ∫ R | f | p ) 1 / p {\textstyle \|f\|_{p}=\left(\int...

{\displaystyle L^{p}(X)} consists of (equivalence classes of) all Bochner measurable functions f {\displaystyle f} with values in the Banach space X {\displaystyle...

every n > N and for every measurable set A. As before, this implies convergence of integrals against bounded measurable functions, but this time convergence...

is similar but is applied to a non-negative measurable function rather than to an integrable function over its domain. The Fubini and Tonelli theorems...

a stationary set of measurable cardinals, and thus it is a Mahlo cardinal. However, the first Woodin cardinal is not even weakly compact. The hierarchy...

logicians, give precise definitions for these weakly specified functions. These generalized functions may be critical in the development of a formalization...

called weakly measurable if for all φ ∈ V ′ , {\displaystyle \varphi \in V',} the scalar-valued map φ ∘ f {\displaystyle \varphi \circ f} is a measurable map...

space – Type of topological space Bochner measurable function Pettis integral Vector measure Weakly measurable function Ardent, Wolfgang; Batty, Charles J.K;...

continuous at each θ ∈ Θ for almost all xs, and measurable function of x at each θ. there exists a dominating function d(x) such that E[d(X)] < ∞, and ‖ f ( x...

theorem relates the weak convergence of cumulative distribution functions to the convergence of expectations of certain measurable functions. It is named after...

non-measurable sets, which states that there exists a subset of the real numbers that is not Lebesgue measurable. There exist Lebesgue-measurable subsets...

Continuity: for every profile v, the set of profiles weakly better than v and the set of profiles weakly worse than v are closed sets.[jargon] 4. Independence...

(f(x)\in F(x))\,.} The existence of more regular choice functions, namely continuous or measurable selections is important in the theory of differential...

the collector) then a measurable electric current will be observed. Thermionic emission can be used to measure the work function of both the hot emitter...

{\displaystyle \circ } takes two functions, f {\displaystyle f} and g {\displaystyle g} , and returns a new function h ( x ) := ( g ∘ f ) ( x ) = g (...

subsets of the Cantor space are measurable and have the property of Baire and thus that no infinite parity function exists; this holds in the Solovay...

}}_{\geq 0}})} -measurable non-negative functions f n : X → [ 0 , + ∞ ] {\displaystyle f_{n}:X\to [0,+\infty ]} . Define the function f : X → [ 0 , +...

a measurable space. A function between two measurable spaces is called a measurable function if the preimage of every measurable set is measurable. The...

In mathematical complex analysis, a quasiconformal mapping is a (weakly differentiable) homeomorphism between plane domains which to first order takes...

} This condition is only slightly weaker than convexity. For example, a real-valued Lebesgue measurable function that is midpoint-convex is convex: this...

mixing implies weak mixing. Furthermore, weak mixing (and thus also strong mixing) implies ergodicity: that is, every system that is weakly mixing is also...

sets in K. If L=K, these are simply the primitive recursive functions. If K has no measurable cardinals, then for every uncountable set x of ordinals, there...