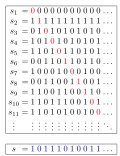
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set...

In mathematics, injections, surjections, and bijections are classes of functions distinguished by the manner in which arguments (input expressions from...

In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f : V ( G ) → V ( H ) {\displaystyle f\colon V(G)\to...

uncountable. Also, by using a method of construction devised by Cantor, a bijection will be constructed between T and R. Therefore, T and R have the same...

is that no bijection can exist between {1, 2, ..., n} and {1, 2, ..., m} unless n = m; this fact (together with the fact that two bijections can be composed...

(surjection, not a bijection) An injective surjective function (bijection) An injective non-surjective function (injection, not a bijection) A non-injective...

In projective geometry, a collineation is a one-to-one and onto map (a bijection) from one projective space to another, or from a projective space to itself...

set is Dedekind-finite if it is not Dedekind-infinite (i.e., no such bijection exists). Proposed by Dedekind in 1888, Dedekind-infiniteness was the first...

In mathematics, a geometric transformation is any bijection of a set to itself (or to another such set) with some salient geometrical underpinning, such...

f(x)=2x} is a bijection from [ 0 , 1 ] {\displaystyle [0,1]} to [ 0 , 2 ] {\displaystyle [0,2]} . Then, the tangent function is a bijection from the interval...

pattern 231; they are counted by the Catalan numbers, and may be placed in bijection with many other combinatorial objects with the same counting function...

states that continuous bijections of smooth manifolds preserve dimension. That is, there does not exist a continuous bijection between two smooth manifolds...

and B are equinumerous if there exists a one-to-one correspondence (or bijection) between them, that is, if there exists a function from A to B such that...

Two sets are shown to have the same number of members by exhibiting a bijection, i.e. a one-to-one correspondence, between them. The term "combinatorial...

other sets that are easier to count. Additionally, the nature of the bijection itself often provides powerful insights into each or both of the sets...

(injection, not a bijection) An injective surjective function (bijection) A non-injective surjective function (surjection, not a bijection) A non-injective...

This bijection then expands to the bijection X = A + B + A + B + ⋯ + Z. Substituting the right hand side for X in Y = B + X gives the bijection Y = B...

same order type if they are order isomorphic, that is, if there exists a bijection (each element pairs with exactly one in the other set) f : X → Y {\displaystyle...

simply a strictly increasing bijection. This result implies, for example, that there exists a strictly increasing bijection between the set of all rational...

same cardinality if, and only if, there is a one-to-one correspondence (bijection) between the elements of the two sets. In the case of finite sets, this...

the integers and the even integers into a one-to-one correspondence (or bijection), which is a function that maps between two sets such that each element...

{\displaystyle f} is a bijection between its elements in A and its elements in B. For a B-stopper, the function g {\displaystyle g} is a bijection between its elements...

mathematical analysis, an isomorphism between two Hilbert spaces is a bijection preserving addition, scalar multiplication, and inner product. In early...

a group isomorphism is a function between two groups that sets up a bijection between the elements of the groups in a way that respects the given group...

partial permutation, or sequence without repetition, on a finite set S is a bijection between two specified subsets of S. That is, it is defined by two subsets...

functions and the solution of recurrence relations. The field involves bijections, power series and formal Laurent series. Gessel, Ira M.; Stanley, Richard...

a given set S of n elements in some fixed order, which establishes a bijection from an interval of ( n k ) {\displaystyle {\tbinom {n}{k}}} integers...

element of G. For an infinite group G {\displaystyle G} , there is still a bijection: G × X / G   ⟷   ∐ g ∈ G X g . {\displaystyle G\times X/G\ \longleftrightarrow...

of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In general, some collineations...

In combinatorial mathematics, a picture is a bijection between skew diagrams satisfying certain properties, introduced by Zelevinsky (1981) in a generalization...