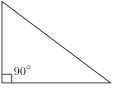
The Calabi triangle is a special triangle found by Eugenio Calabi and defined by its property of having three different placements for the largest square...

between them, must lie on one of the sides of the triangle. For instance, for the Calabi triangle depicted, the square with horizontal and vertical sides...

relation is the Calabi triangle in which the vertices of every three squares are tangent to all obtuse triangle's sides. Every acute triangle has three inscribed...

isosceles right triangle, several other specific shapes of isosceles triangles have been studied. These include the Calabi triangle (a triangle with three...

acute triangle (or acute-angled triangle) is a triangle with three acute angles (less than 90°). An obtuse triangle (or obtuse-angled triangle) is a triangle...

Eugenio Calabi (May 11, 1923 – September 25, 2023) was an Italian-born American mathematician and the Thomas A. Scott Professor of Mathematics at the University...

Squares can be inscribed in any smooth or convex curve such as a circle or triangle, but it remains unsolved whether a square can be inscribed in every simple...

compactified space must be a 6-dimensional Calabi–Yau manifold. There are a large number of possible Calabi–Yau manifolds (tens of thousands), hence the...

to be proven with great success, including Shing-Tung Yau's proof of the Calabi conjecture, the Hitchin–Kobayashi correspondence, the nonabelian Hodge correspondence...

contributions to quantum gravity and string theory. These include his work on Calabi–Yau compactification and topology change in string theory, and on the stringy...

physics, the compact extra dimensions must be shaped like a Calabi–Yau manifold. A Calabi–Yau manifold is a special space which is typically taken to...

homological mirror symmetry conjecture predicts that the derived category of a Calabi–Yau manifold is equivalent to the Fukaya category of its "mirror" symplectic...

examples of spaces studied in complex geometry include Riemann surfaces, and Calabi–Yau manifolds, and these spaces find uses in string theory. In particular...

that mirror to a symplectic manifold (which is a Calabi–Yau manifold) there should be another Calabi–Yau manifold for which the symplectic structure is...

six-dimensional Calabi–Yau manifold. This is a special kind of geometric object named after mathematicians Eugenio Calabi and Shing-Tung Yau. Calabi–Yau manifolds...

superstring theory requires six compact dimensions (6D hyperspace) forming a Calabi–Yau manifold. Thus Kaluza-Klein theory may be considered either as an incomplete...

polyhedron models Jean-Louis Koszul (1921–2018) Isaak Yaglom (1921–1988) Eugenio Calabi (1923–2023) Benoit Mandelbrot (1924–2010) – fractal geometry Katsumi Nomizu...

the fundamental Laplacian comparison theorem proved earlier by Eugenio Calabi, these functions are both superharmonic under the Ricci curvature assumption...

homology of Lagrangians in a Calabi–Yau manifold X {\displaystyle X} and the Ext groups of coherent sheaves on the mirror Calabi–Yau manifold. In this situation...

space Base space Bergman space Berkovich space Besov space Borel space Calabi-Yau space Cantor space Cauchy space Cellular space Chu space Closure space...

label), bladder cancer. Eugenio Calabi, 100, Italian-born American mathematician (Calabi conjecture, Calabi–Yau manifold, Calabi flow). Bob Dahl, 54, American...

triangulated category is the derived category of coherent sheaves on a Calabi–Yau manifold, and this situation has fundamental links to string theory...

Ruddat, Helge; Thompson, Alan (2015). "An Introduction to Hodge Structures". Calabi-Yau Varieties: Arithmetic, Geometry and Physics. Fields Institute Monographs...

 p. 160 Harris, M.; Shepherd-Barron, N.; Taylor, R. (2010). "A family of Calabi–Yau varieties and potential automorphy". Annals of Mathematics. 171 (2):...

{\displaystyle X} is Calabi-Yau, since ω X ≅ O X {\displaystyle \omega _{X}\cong {\mathcal {O}}_{X}} , or is the product of a variety which is Calabi-Yau. Abelian...

smooth projective Calabi–Yau variety of dimension d then D b ( Coh ⁡ ( X ) ) {\displaystyle D^{b}(\operatorname {Coh} (X))} is a unital Calabi–Yau A∞-category...

remark in a paper by André Weil; various other authors such as Lorenzo Calabi, Wu Wen-tsün, and Nodar Berikashvili have also published proofs. In the...

professor of mathematics, Morningside Gold Medal of Mathematics (1998) Eugenio Calabi (Ph.D., 1950) – professor emeritus, University of Pennsylvania; Leroy P...

Monge-Ampere equations. This was the main step in the proof of the existence of Calabi-Yau manifolds, which play an important role in theoretical physics. A Monge-Ampère...

_{n}(\mathbb {R} )} . Shortly afterwards a similar statement was proven by Eugenio Calabi in the setting of fundamental groups of compact hyperbolic manifolds. Finally...