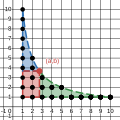
In mathematics, Dirichlet convolution (or divisor convolution) is a binary operation defined for arithmetic functions; it is important in number theory...

matrix Convolution for optical broad-beam responses in scattering media Convolution power Convolution quotient Deconvolution Dirichlet convolution Generalized...

function, so called because it is the multiplicative identity for Dirichlet convolution. Sometimes written as u ( n ) {\displaystyle u(n)} ; not to be confused...

f(p)a f(q)b ... While the Dirichlet convolution of two multiplicative functions is multiplicative, the Dirichlet convolution of two completely multiplicative...

obtained by applying Möbius inversion and Dirichlet convolution to known series. For example, given a Dirichlet character χ(n) one has 1 L ( χ , s ) = ∑...

is called the Dirichlet convolution of a and b, and is denoted by a ∗ b {\displaystyle a*b} . A particularly important case is convolution with the constant...

(s-a-b)}{\zeta (2s-a-b)}},} which is a special case of the Rankin–Selberg convolution. A Lambert series involving the divisor function is: ∑ n = 1 ∞ q n σ...

divisors of a natural number n {\displaystyle n} , or equivalently the Dirichlet convolution of an arithmetic function f ( n ) {\displaystyle f(n)} with one:...

mathematics, convolution is a binary operation on functions. Circular convolution Convolution theorem Titchmarsh convolution theorem Dirichlet convolution Infimal...

using Dirichlet convolution as: 1 ∗ μ = ε {\displaystyle 1*\mu =\varepsilon } where ε {\displaystyle \varepsilon } is the identity under the convolution. One...

In probability and statistics, the Dirichlet distribution (after Peter Gustav Lejeune Dirichlet), often denoted Dir ⁡ ( α ) {\displaystyle \operatorname...

{\displaystyle 2\pi } . The importance of the Dirichlet kernel comes from its relation to Fourier series. The convolution of Dn(x) with any function f of period...

of Dirichlet convolutions, the first formula may be written as g = 1 ∗ f {\displaystyle g={\mathit {1}}*f} where ∗ denotes the Dirichlet convolution, and...

find a pair of multiplicative functions g and h such that, using Dirichlet convolution, we have f = g ∗ h; the sum then becomes F ( n ) = ∑ k = 1 n ∑ x...

an inverse f − 1 ( n ) {\displaystyle f^{-1}(n)} with respect to Dirichlet convolution such that ( f ∗ f − 1 ) ( n ) = δ n , 1 {\displaystyle (f\ast f^{-1})(n)=\delta...

{\displaystyle g} , let h = f ∗ g {\displaystyle h=f*g} be their Dirichlet convolution. Then for every prime p {\displaystyle p} , one has: h p ( x ) =...

called the unit function because it is the identity element for Dirichlet convolution. It may be described as the "indicator function of 1" within the...

Dirichlet hyperbola method re-expresses a sum of a multiplicative function f ( n ) {\displaystyle f(n)} by selecting a suitable Dirichlet convolution...

ordered by divisibility The convolution associated to the incidence algebra for intervals [1, n] becomes the Dirichlet convolution, hence the Möbius function...

1831) Dirichlet conditions (Fourier series) Dirichlet convolution (number theory and arithmetic functions) Dirichlet density (number theory) Dirichlet average...

Bell series, and Dirichlet series. Every sequence in principle has a generating function of each type (except that Lambert and Dirichlet series require...

} This is also a consequence of the fact that we can write as a Dirichlet convolution of ψ = I d ∗ | μ | {\displaystyle \psi =\mathrm {Id} *|\mu |} ....

j = 1; otherwise, aij = 0. It is useful in some contexts to express Dirichlet convolution, or convolved divisors sums, in terms of matrix products involving...

}b_{m}q^{m}} where the coefficients of the new series are given by the Dirichlet convolution of an with the constant function 1(n) = 1: b m = ( a ∗ 1 ) ( m )...

and Iwaniec generalized the Elliott-Halberstam conjecture, using Dirichlet convolution of arithmetic functions related to the von Mangoldt function. The...

partial differential equations, and to perform other operations such as convolutions or multiplying large integers. Since it deals with a finite amount of...

Jean-Marc Champarnaud et al, Université de Rouen, France PDF "Dirichlet convolution and enumeration of pyramid polycubes", C. Carré, N. Debroux, M....

well-defined. The polynomials for M and N are easily related in terms of Dirichlet convolution of arithmetic functions f ( n ) ∗ g ( n ) {\displaystyle f(n)*g(n)}...

begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic progressions...

expresses the Fejér kernel F n ( x ) {\displaystyle F_{n}(x)} in terms of the Dirichlet kernel: F n ( x ) = 1 n ∑ k = 0 n − 1 D k ( x ) {\displaystyle F_{n}(x)={\frac...