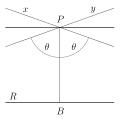
In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski, is a model of n-dimensional hyperbolic geometry in which...

some regions, where they locally resemble the hyperbolic plane. The hyperboloid model of hyperbolic geometry provides a representation of events one temporal...

 xn] on the upper sheet of the hyperboloid of the hyperboloid model, thereby defining a point in the hyperboloid model, we may project it onto the hyperplane...

In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal...

hyperboloid model is immediate through the action of the connected component of S O ( n , 1 ) {\displaystyle \mathrm {SO} (n,1)} on the hyperboloid....

half-plane model can be thought of as a map projection from the curved hyperbolic plane to the flat Euclidean plane. From the hyperboloid model (a representation...

projection of the hyperboloid model (Hy) with as center the center of the hyperboloid (O) and the projection plane tangent to the hyperboloid. Given two distinct...

cases of Apollonius' problem. In the hyperboloid model horocycles are represented by intersections of the hyperboloid with planes that generate parabolas...

model (but rays parallel to the positive y-axis approach it). In the hyperboloid model there are no ideal points. Ideal triangle Ideal polyhedron Points...

the hyperboloid model of the hyperbolic plane, the hyperboloid is referred to as a pseudosphere. This usage of the word is because the hyperboloid can...

as Minkowski did in 1908. The relevant structure is now called the hyperboloid model of hyperbolic geometry. The non-Euclidean planar algebras support...

the complex plane. Hyperbolic motions can also be described on the hyperboloid model of hyperbolic geometry. This article exhibits these examples of the...

{\displaystyle ~p\neq \pm i~} . The Poincaré sphere model used since 1892 has been compared to a 2-sheet hyperboloid model, and the practice of SU(1, 1) interferometry...

The mathematical basis of Minkowski space can also be found in the hyperboloid model of hyperbolic space already known in the 19th century, because isometries...

horizon plane, or as a plane parallel to the horizon plane. In the hyperboloid model, a horosphere is represented by a plane whose normal lies in the asymptotic...

representation Clebsch surface Eigenvalues and eigenvectors Helmholtz equation Hyperboloid model Pentagram map Quaternary cubic "Prix". Comptes rendus hebdomadaires...

excess hyperbolic geometry hyperbolic space hyperboloid model Poincaré disc model Poincaré half-plane model Poincaré metric Angle of parallelism Prime...

1885. Recounting lectures of Weierstrass, he there introduced the hyperboloid model of hyperbolic geometry described by Weierstrass coordinates. He is...

four-gradient four-momentum four-velocity hyperbolic orthogonality hyperboloid model light-like Lorentz covariance Lorentz group Lorentz transformation...

Four-gradient Algebra of physical space Congruence (general relativity) Hyperboloid model Rapidity Technically, the four-vector should be thought of as residing...

Lorentz group, point stabilizer orthogonal group, corresponding to hyperboloid model): Hn ≅ O+(1, n) / O(n) Oriented hyperbolic space: SO+(1, n) / SO(n)...

the scalar curvature is S = n(n − 1)/r2. Hyperbolic space By the hyperboloid model, an n-dimensional hyperbolic space can be identified with the subset...

computational mathematics competition Mathlete Parametric surface Procedural modeling suites Ray tracing Tesseract 3Blue1Brown - math Youtube channel https://design...

been described by other models such as the Klein model or the hyperboloid model, obtained by considering the two-sheeted hyperboloid q(x, y, z) = −1 in three-dimensional...

_{R}^{1(n)}} is a Riemannian manifold. It is one of the model spaces of Riemannian geometry, the hyperboloid model of hyperbolic space. It is a space of constant...

hyperbolic rotations. Pseudo-Riemannian manifold Hyperbolic equation Hyperboloid model Paravector Élie Cartan (1981), The Theory of Spinors, Dover Publications...

model for hyperbolic space H3 on the hyperboloid H 3 = { q ∈ M : q ( q ∗ ) = 1 } . {\displaystyle H^{3}=\{q\in M:q(q^{*})=1\}.} This isotropic model is...

the metric structure of a hyperbolic space, in particular it is the hyperboloid model of hyperbolic space, see geometry of Minkowski space for proof. The...

frame. In 1881 Poincaré described hyperbolic geometry in terms of the hyperboloid model, formulating transformations leaving invariant the Lorentz interval...

Minkowski space restricts to the isometric action of PSL(2, R) on the hyperboloid model of the hyperbolic plane. The eigenvalues of an element A ∈ SL(2, R)...