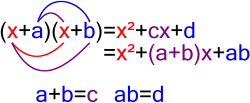prime factorization; the result is always unique up to the order of the factors by the prime factorization theorem. To factorize a small integer n using...

Integer factorization is the process of determining which prime numbers divide a given positive integer. Doing this quickly has applications in cryptography...

For example, 3 × 5 is an integer factorization of 15, and (x − 2)(x + 2) is a polynomial factorization of x2 − 4. Factorization is not usually considered...

arithmetic, also called the unique factorization theorem and prime factorization theorem, states that every integer greater than 1 can be represented uniquely...

Fermat's factorization method, named after Pierre de Fermat, is based on the representation of an odd integer as the difference of two squares: N = a 2...

square-free integers that are pairwise coprime. This is called the square-free factorization of n. To construct the square-free factorization, let n = ∏...

followed either by an explicit factorization or followed by the label (p) if the integer is a Gaussian prime. The factorizations take the form of an optional...

circuits. In 2012, the factorization of 15 {\displaystyle 15} was performed with solid-state qubits. Later, in 2012, the factorization of 21 {\displaystyle...

and encryption schemes using several mathematical approaches: integer factorization, discrete logarithm, and elliptic curve discrete logarithm. DL/ECKAS-DH1...

algebra, factorization of polynomials or polynomial factorization expresses a polynomial with coefficients in a given field or in the integers as the product...

unique factorization and many related properties. However, Gaussian integers do not have a total order that respects arithmetic. Gaussian integers are algebraic...

factoring large integers on a classical computer has yet been found, but it has not been proven that none exists; see integer factorization for a discussion...

decimal digits (330 bits). Its factorization was announced on April 1, 1991, by Arjen K. Lenstra. Reportedly, the factorization took a few days using the multiple-polynomial...

example). This asymmetry is analogous to the one between integer factorization and integer multiplication. Both asymmetries (and other possibly one-way...

theory, Dixon's factorization method (also Dixon's random squares method or Dixon's algorithm) is a general-purpose integer factorization algorithm; it...

whether there is a polynomial-time algorithm for factorization, equivalently that integer factorization is in P, and hence this example is interesting as...

Arithmetic functions Euclidean algorithm Fraction (mathematics) Integer factorization Table of divisors – A table of prime and non-prime divisors for...

Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not. Factorization is...

polynomial time. The decision problem version of the integer factorization problem: given integers n and k, is there a factor f with 1 < f < k and f dividing...

used in several integer factorization algorithms that have applications in cryptography, such as Lenstra elliptic-curve factorization. The use of elliptic...

Pollard's rho algorithm is an algorithm for integer factorization. It was invented by John Pollard in 1975. It uses only a small amount of space, and...

elliptic-curve factorization or the elliptic-curve factorization method (ECM) is a fast, sub-exponential running time, algorithm for integer factorization, which...

is a congruence commonly used in integer factorization algorithms. Given a positive integer n, Fermat's factorization method relies on finding numbers...

quasi-polynomial time. The integer factorization problem is the computational problem of determining the prime factorization of a given integer. Phrased as a decision...

cryptographic systems. Shor's algorithm, a quantum algorithm for integer factorization, could potentially break widely used public-key encryption schemes...

Prime factors calculator can factorize any positive integer up to 20 digits. Fast Online primality test with factorization makes use of the Elliptic Curve...

, is fundamental in number theory. It is used in cryptography, integer factorization, and primality testing. It is an abelian, finite group whose order...

The quadratic sieve algorithm (QS) is an integer factorization algorithm and, in practice, the second-fastest method known (after the general number field...

In number theory, the continued fraction factorization method (CFRAC) is an integer factorization algorithm. It is a general-purpose algorithm, meaning...

{a}{n/2}}\right)=1} , the problem is known to be equivalent to integer factorization of n (i.e. an efficient solution to either problem could be used...