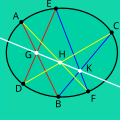
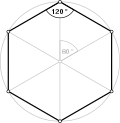
In projective geometry, Pascal's theorem (also known as the hexagrammum mysticum theorem, Latin for mystical hexagram) states that if six arbitrary points...

entries in Pascal's triangle (Singmaster's conjecture) Pascal matrix Pascal's pyramid Pascal's simplex Proton NMR, one application of Pascal's triangle...

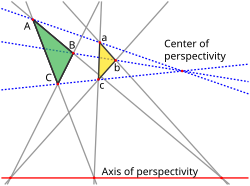
projective dual of this theorem give Pascal's theorem. As for Pascal's theorem there exist degenerations for Brianchon's theorem, too: Let coincide two...

{\displaystyle Y_{\infty }} . The 5-, 4- and 3- point degenerations of Pascal's theorem are properties of a conic dealing with at least one tangent. If one...

Braikenridge–Maclaurin theorem, named for 18th-century British mathematicians William Braikenridge and Colin Maclaurin, is the converse to Pascal's theorem. It states...

Pappus's theorem is a special case of Pascal's theorem for a conic—the limiting case when the conic degenerates into 2 straight lines. Pascal's theorem is in...

sides lie on a line (called the Pascal line). Pascal's work was so precocious that René Descartes was convinced that Pascal's father had written it. When...

a projective plane in which the little Desargues theorem is valid for every line. Pascal's theorem Smith (1959, p. 307) Katz (1998, p. 461) (Coxeter...

{\displaystyle n} ⁠ and ⁠ k {\displaystyle k} ⁠ can be arranged to form Pascal's triangle. These numbers also occur in combinatorics, where ⁠ ( n k ) {\displaystyle...

20 points associated with a given set of six points on a conic; see Pascal's theorem § Hexagrammum Mysticum Steiner tree problem, an algorithmic problem...

by applying the Braikenridge–Maclaurin theorem, which is the converse of Pascal's theorem. Pascal's theorem states that given 6 points on a conic (a...

suitable ellipse smoothly. The proof of Segre's theorem, shown below, uses the 3-point version of Pascal's theorem and a property of a finite field of odd order...

Brianchon's theorem Ceva's theorem Desargues's theorem Menelaus's theorem Pascal's theorem Poncelet's closure theorem Ptolemy's theorem Apollonian circles...

}}=34650.} One can use the multinomial theorem to generalize Pascal's triangle or Pascal's pyramid to Pascal's simplex. This provides a quick way to generate...

Pascal's theorem concerns the collinearity of three points that are constructed from a set of six points on any non-degenerate conic. The theorem also...

sections drew the attention of 16-year-old Blaise Pascal and helped him formulate Pascal's theorem. The works of Gaspard Monge at the end of 18th and...

Duality Homogeneous coordinates Pappus's hexagon theorem Incidence Pascal's theorem Affine geometry Affine space Affine transformation Finite geometry...

theorem (geometry) Pascal's theorem (conics) Pasch's theorem (order theory) Pitot theorem (plane geometry) Pivot theorem (circles) Pompeiu's theorem (Euclidean...

the Conway criterion will tile the plane. Pascal's theorem (also known as the "Hexagrammum Mysticum Theorem") states that if an arbitrary hexagon is inscribed...

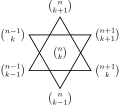
coefficients forming each of the two triangles in the Star of David shape in Pascal's triangle are equal: gcd { ( n − 1 k − 1 ) , ( n k + 1 ) , ( n + 1 k ) }...

(without seven co-conic ones) are already prescribed. A special case is Pascal's theorem, in which case the two cubics in question are all degenerate: given...

of a hyperbola is an affine version of the 3-point-degeneration of Pascal's theorem. Area of the grey parallelogram The area of the grey parallelogram...

the legs are collinear with the incenter. Pascal's theorem (also known as the Hexagrammum Mysticum Theorem) states that if an arbitrary six points are...

the angles formed where the extensions of opposite sides intersect. Pascal's theorem states that if six arbitrary points are chosen on a conic section (i...

Historically, advanced Euclidean geometry, including theorems like Pascal's theorem and Brianchon's theorem, was integral to drafting practices. However, with...

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle...

Automated theorem proving (also known as ATP or automated deduction) is a subfield of automated reasoning and mathematical logic dealing with proving...

in the September Number of this Journal "On a new Class of Theorem" and "On Pascal's Theorem"". London, Edinburgh, and Dublin Philosophical Magazine. 37:...

In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers a, b...

product of projective spaces Rational normal curve Conics, Pascal's theorem, Brianchon's theorem Twisted cubic Elliptic curve, cubic curve Elliptic function...