mathematics, the power set (or powerset) of a set S is the set of all subsets of S, including the empty set and S itself. In axiomatic set theory (as developed...

the common usage of sets in mathematics does not require the full power of Zermelo–Fraenkel set theory. In mathematical practice, sets can be manipulated...

constructions in set theory, such as the power set of a set A, which is the set of all possible subsets of A. He later proved that the size of the power set of A...

of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory. It guarantees for every set x {\displaystyle x} the existence of a set P (...

where Z 0 {\displaystyle Z_{0}} is any infinite set and P {\displaystyle {\mathcal {P}}} is the power set operation. Moreover, one of Zermelo's axioms invoked...

In set theory, the complement of a set A, often denoted by A c {\displaystyle A^{c}} (or A′), is the set of elements not in A. When all elements in the...

union is infinite. The power set of an infinite set is infinite. Any superset of an infinite set is infinite. If an infinite set is partitioned into finitely...

itself; equivalently, the power set of the empty set is the set containing only the empty set. The number of elements of the empty set (i.e., its cardinality)...

that set, where P {\displaystyle {\mathcal {P}}} represents the power set operator. Therefore, the existence of the Cartesian product of any two sets in...

mathematics, particularly set theory, a finite set is a set that has a finite number of elements. Informally, a finite set is a set which one could in principle...

mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is countable...

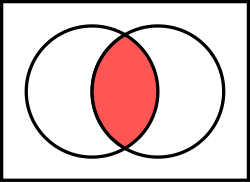
In set theory, the intersection of two sets A {\displaystyle A} and B , {\displaystyle B,} denoted by A ∩ B , {\displaystyle A\cap B,} is the set containing...

empty set are also members of any set A is vacuously true). The set of all subsets of a given set A is called the power set of A and is denoted by 2 A {\displaystyle...

In set theory, the union (denoted by ∪) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations...

domain is called the universe denoted U. The range is the set of subsets of U called the power set of U and denoted P(U). Thus the relation ∈ {\displaystyle...

addition modulo 2. The power set of any set becomes an abelian group under the operation of symmetric difference, with the empty set as the neutral element...

2^{-2}} is a quarter. Powers of 2 appear in set theory, since a set with n members has a power set, the set of all of its subsets, which has 2n members...

{Z} ,n=2k\}} The set of all even integers, expressed in set-builder notation. In mathematics and more specifically in set theory, set-builder notation...

In computability theory, a set of natural numbers is computable (or decidable or recursive) if there is an algorithm that computes the membership of every...

mathematics, an uncountable set, informally, is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related...

between sets, popularized by John Venn (1834–1923) in the 1880s. The diagrams are used to teach elementary set theory, and to illustrate simple set relationships...

"algebra" in measure theory.) One example of a Boolean ring is the power set of any set X, where the addition in the ring is symmetric difference, and the...

set concerns the power set of the set of all sets. Because this power set is a set of sets, it would necessarily be a subset of the set of all sets,...

built up from the empty set by transfinitely iterating the power set operation. It is thus now possible again to reason about sets in a non-axiomatic fashion...

(or power) than the former set. Another example in an Euler diagram: A is a proper subset of B. C is a subset but not a proper subset of B. The set of...

of families of sets satisfying certain restrictions. The set of all subsets of a given set S {\displaystyle S} is called the power set of S {\displaystyle...

algebra of sets, not to be confused with the mathematical structure of an algebra of sets, defines the properties and laws of sets, the set-theoretic operations...

In set theory and its applications throughout mathematics, a class is a collection of sets (or sometimes other mathematical objects) that can be unambiguously...

theorem). They include, for instance: the set of all subsets of R, i.e., the power set of R, written P(R) or 2R the set RR of all functions from R to R Both...

IBM POWER is a reduced instruction set computer (RISC) instruction set architecture (ISA) developed by IBM. The name is an acronym for Performance Optimization...