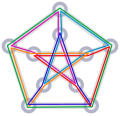
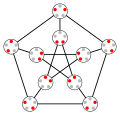
In graph theory, Vizing's theorem states that every simple undirected graph may be edge colored using a number of colors that is at most one larger than...

colored by two colors, so the graph shown has chromatic index three. By Vizing's theorem, the number of colors needed to edge color a simple graph is either...

result that the chromatic index is at most Δ + 1 is Vizing's theorem. An extension of Brooks' theorem to total coloring, stating that the total chromatic...

for all others. The existence of such a coloring is guaranteed by Vizing's theorem. It was first published by Jayadev Misra and David Gries in 1992. It...

See vertex. Vizing 1.  Vadim G. Vizing 2.  Vizing's theorem that the chromatic index is at most one more than the maximum degree. 3.  Vizing's conjecture...

relationship is even stronger than what Brooks's theorem gives for vertex coloring: Vizing's Theorem: A graph of maximal degree Δ {\displaystyle \Delta...

minimum number of colors in a proper edge-coloring of a graph, and Vizing's theorem states that the chromatic index of a graph G {\displaystyle G} is either...

especially for Vizing's theorem stating that the edges of any simple graph with maximum degree Δ can be colored with at most Δ + 1 colors. Vizing was born in...

exactly 1. By Brooks' theorem, any graph G other than a clique or an odd cycle has chromatic number at most Δ(G), and by Vizing's theorem any graph has chromatic...

class in a 3-coloring has at least this many vertices. According to Vizing's theorem every cubic graph needs either three or four colors for an edge coloring...

color different from the colors of its two neighbors. According to Vizing's theorem, the chromatic index of any graph (the minimum number of colors needed...

bipartite graphs, is another theorem of Dénes Kőnig. In arbitrary simple graphs, they can differ by one; this is Vizing's theorem. The underlying graph G {\displaystyle...

each vertex) whose edges cannot be colored with only three colors. By Vizing's theorem, the number of colors needed for the edges of a cubic graph is either...

perfect matchings (that is, the graph has no 3-edge coloring, and by Vizing's theorem has chromatic index 4). It turns out that snarks form the only difficult...

graphs have chromatic index 3. These are the only possibilities, by Vizing's theorem. The generalized Petersen graph G ( 9 , 2 ) {\displaystyle G(9,2)}...

and two more colors suffice to color the complementary matching. By Vizing's theorem, the number of colors needed to color the edges of the odd graph O...

{\displaystyle \chi } -bounded, as Ramsey's theorem implies that they have large cliques. Vizing's theorem can be interpreted as stating that the line...

{\frac {3}{2}}\Delta } colors in any proper edge coloring. A version of Vizing's theorem states that every multigraph with maximum degree Δ {\displaystyle \Delta...

shoe strike began in Maine. Born: Vadim G. Vizing, Soviet Ukrainian mathematician known for Vizing's theorem; in Kiev (d. 2017) Died: Georges Valmier,...

multigraph and can have loops. For simple graphs, this result follows from Vizing's theorem. It is already known that for loopless G (but can have parallel edges):...

triangles be hit by a set of at most 2 ν {\displaystyle 2\nu } edges? Vizing's conjecture on the domination number of cartesian products of graphs Zarankiewicz...

as of September 2022[update]. The conjecture terminology may persist: theorems often enough may still be referred to as conjectures, using the anachronistic...

Cornell University best known for the eponymous Hohenberg–Mermin–Wagner theorem, his application of the term "boojum" to superfluidity, his textbook with...

allowed colors. It was first studied in the 1970s in independent papers by Vizing and by Erdős, Rubin, and Taylor. Given a graph G and given a set L(v) of...

Sabidussi (1960). Hahn & Sabidussi (1997). Sabidussi (1960); Vizing (1963). Imrich & Klavžar (2000), Theorem 4.19. Sabidussi (1957). Horvat & Pisanski (2010). Imrich...

Krein–Milman theorem and Krein space, Wolf Prize winner Nikolay Krylov, author of the edge-of-the-wedge theorem, Krylov–Bogolyubov theorem and describing...

University of Cologne with thesis Asymptotic Expansions in the Central Limit Theorem in Banach Spaces under the supervision of Johann Pfanzagl. At the University...

Mikolaiovich Sharkovsky (1936–2022), known for developing Sharkovsky's theorem on the periods of discrete dynamical systems Samuil Shatunovsky (1859–1929)...

triangles and must have maximum vertex degree at least four. Similar to Vizing's conjecture for dominating sets, it is not known whether for all graphs...