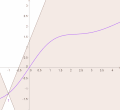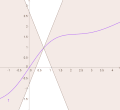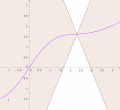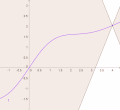
mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of the function lies above or on the graph...

K-convex functions, first introduced by Scarf, are a special weakening of the concept of convex function which is crucial in the proof of the optimality...

In mathematics, a Schur-convex function, also known as S-convex, isotonic function and order-preserving function is a function f : R d → R {\displaystyle...

particular the subfields of convex analysis and optimization, a proper convex function is an extended real-valued convex function with a non-empty domain...

In convex analysis and the calculus of variations, both branches of mathematics, a pseudoconvex function is a function that behaves like a convex function...

Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently...

Bohr-Mollerup Theorem for the gamma function, the log K-function is the unique (up to an additive constant) eventually 2-convex solution to the equation Δ f...

the function) is a convex set. Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex sets...

"sublinear function." Let X {\displaystyle X} be a vector space over a field K , {\displaystyle \mathbb {K} ,} where K {\displaystyle \mathbb {K} } is either...

set of holomorphic functions on G. For a compact set K ⊂ G {\displaystyle K\subset G} , the holomorphically convex hull of K is K ^ G := { z ∈ G ; | f...

Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex...

combinations with positive coefficients. It follows that convex cones are convex sets. The definition of a convex cone makes sense in a vector space over any ordered...

is the unique interpolating function for the factorial, defined over the positive reals, which is logarithmically convex, meaning that y = log ⁡ f ( x...

In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined...

a set K ⊂ Rd is defined to be orthogonally convex if, for every line L that is parallel to one of standard basis vectors, the intersection of K with L...

analysis and related areas of mathematics, locally convex topological vector spaces (LCTVS) or locally convex spaces are examples of topological vector spaces...

self-concordant barrier is a particular self-concordant function, that is also a barrier function for a particular convex set. Self-concordant barriers are important...

all real-valued Lipschitz functions on a compact metric space X having Lipschitz constant ≤ K  is a locally compact convex subset of the Banach space...

In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points...

Invex functions were introduced by Hanson as a generalization of convex functions. Ben-Israel and Mond provided a simple proof that a function is invex...

mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906, building...

minimum under certain assumptions on the function F {\displaystyle F} (for example, F {\displaystyle F} convex and ∇ F {\displaystyle \nabla F} Lipschitz)...

general form than the latter is for continuous functions from a nonempty convex compact subset K {\displaystyle K} of Euclidean space to itself. Among hundreds...

homogeneous function. For example, a homogeneous polynomial of degree k defines a homogeneous function of degree k. The above definition extends to functions whose...

a convex function and G is a convex set. Without loss of generality, we can assume that the objective f is a linear function. Usually, the convex set...

asymptotes as x → ± ∞ {\displaystyle x\rightarrow \pm \infty } . A sigmoid function is convex for values less than a particular point, and it is concave for values...

be a convex function with domain R n . {\displaystyle \mathbb {R} ^{n}.} A classical subgradient method iterates x ( k + 1 ) = x ( k ) − α k g ( k )  ...

need not be positive definite. Seminorms are intimately connected with convex sets: every seminorm is the Minkowski functional of some absorbing disk...

generating functions are positive and log-convex,[citation needed] with M(0) = 1. An important property of the moment-generating function is that it uniquely...

with replacing a non-convex function with its convex closure, that is the function that has the epigraph that is the closed convex hull of the original...