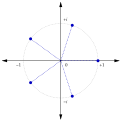
coefficients from an arbitrary field, its reciprocal polynomial or reflected polynomial, denoted by p∗ or pR, is the polynomial p ∗ ( x ) = a n + a n − 1 x + ⋯...
13 KB (1,639 words) - 23:47, 24 April 2025
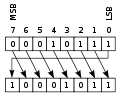
Mathematics of cyclic redundancy checks (section Reversed representations and reciprocal polynomials)
of reciprocal polynomials, when used in CRCs, is that they have exactly the same error-detecting strength as the polynomials they are reciprocals of....
22 KB (3,951 words) - 22:01, 7 February 2025
also known as a reciprocal Reciprocal polynomial, a polynomial obtained from another polynomial by reversing its coefficients Reciprocal rule, a technique...
2 KB (246 words) - 19:18, 25 February 2024
Salem number (redirect from Lehmer's polynomial)
has a root of absolute value 1, the minimal polynomial for a Salem number must be a reciprocal polynomial. This implies that 1 / α {\displaystyle 1/\alpha...
5 KB (895 words) - 18:43, 2 March 2024
Reciprocity (redirect from Reciprocal relationship)
Q Weil reciprocity law Reciprocal polynomials, the coefficients of the remainder polynomial are the bits of the CRC Reciprocal square root Reciprocity...
5 KB (635 words) - 21:54, 20 January 2025
Discriminant (redirect from Discriminant of a polynomial)
precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number...
41 KB (6,704 words) - 19:24, 14 May 2025
Root of unity (category Polynomials)
{1}{z}}} is twice the real part of z. In other words, Φn is a reciprocal polynomial, the polynomial R n {\displaystyle R_{n}} that has r as a root may be deduced...
41 KB (5,944 words) - 11:50, 16 May 2025
multiplicity coincides. Moreover, since the characteristic polynomial of the inverse is the reciprocal polynomial of the original, the eigenvalues share the same...
102 KB (13,617 words) - 15:46, 13 May 2025
and roots of a polynomial Cohn's theorem relating the roots of a self-inversive polynomial with the roots of the reciprocal polynomial of its derivative...
34 KB (5,353 words) - 17:36, 29 September 2024
systems get a short check value attached, based on the remainder of a polynomial division of their contents. On retrieval, the calculation is repeated...
71 KB (5,843 words) - 04:20, 13 April 2025
+a_{n}} be a polynomial. The polynomial whose roots are the reciprocals of the roots of P as roots is its reciprocal polynomial Q ( y ) = y n P (...
7 KB (1,080 words) - 07:55, 13 February 2025
Cohn's theorem (category Theorems about polynomials)
the reciprocal polynomial of its derivative. Cohn's theorem is useful for studying the distribution of the roots of self-inversive and self-reciprocal polynomials...
4 KB (642 words) - 00:03, 17 May 2024
Resultant (redirect from Polynomial resultant)
resultant of two polynomials is a polynomial expression of their coefficients that is equal to zero if and only if the polynomials have a common root...
46 KB (8,057 words) - 16:45, 14 March 2025
factor is irreducible (but not by Eisenstein's criterion). Only the reciprocal polynomial is irreducible by Eisenstein's criterion. We have now shown that...
16 KB (2,541 words) - 10:37, 28 April 2025
Basel problem (redirect from Series of reciprocal squares)
the problem. The Basel problem asks for the precise summation of the reciprocals of the squares of the natural numbers, i.e. the precise sum of the infinite...
44 KB (8,670 words) - 03:32, 4 May 2025
The reciprocals of prime numbers have been of interest to mathematicians for various reasons. They do not have a finite sum, as Leonhard Euler proved...
10 KB (750 words) - 16:17, 23 January 2025
g(x)h^{*}(x)=x^{n}-1} , where h ∗ ( x ) {\displaystyle h^{*}(x)} denotes the reciprocal polynomial of h ( x ) {\displaystyle h(x)} . The idempotent of C {\displaystyle...
27 KB (5,187 words) - 01:11, 9 May 2025
} The associated Narayana polynomial N n ( z ) {\displaystyle {\mathcal {N}}_{n}(z)} is defined as the reciprocal polynomial of N n ( z ) {\displaystyle...
5 KB (1,096 words) - 08:23, 8 January 2025
for higher order polynomial equations. If there are more than n + 1 constraints (n being the degree of the polynomial), the polynomial curve can still...
17 KB (2,144 words) - 12:58, 6 May 2025
quadratic polynomial, the only ways to rearrange two roots are to either leave them be or to transpose them, so solving a quadratic polynomial is simple...
35 KB (5,773 words) - 10:22, 17 May 2025
Golden ratio (section Minimal polynomial)
an algebraic integer. It has minimal polynomial x 2 − x − 1. {\displaystyle x^{2}-x-1.} This quadratic polynomial has two roots, φ {\displaystyle \varphi...
114 KB (13,221 words) - 17:08, 30 April 2025
Bernoulli's method (category Polynomial factorization algorithms)
smallest absolute value, one can apply the method on the reciprocal polynomial (polynomial obtained by reversing the order of the coefficients), and...
27 KB (3,419 words) - 07:10, 17 May 2025
orthogonal polynomials is zero by virtue of their mutual orthogonality. Therefore, each non-zero element of its inverse is simply the reciprocal the corresponding...
54 KB (8,147 words) - 21:57, 28 April 2025
algebra, completing the square is a technique for converting a quadratic polynomial of the form a x 2 + b x + c {\displaystyle \textstyle ax^{2}+bx+c} ...
22 KB (3,686 words) - 04:33, 25 March 2025
location polynomial. The roots of the error location polynomial can be found by exhaustive search. The error locators Xk are the reciprocals of those...
75 KB (12,395 words) - 16:42, 29 April 2025
on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions...
18 KB (3,285 words) - 13:28, 29 March 2025
complexity that is polynomial in both the size of the input and in the reciprocal of the relative error, 1/η (rather than being polynomial merely in log(1/η)...
20 KB (2,701 words) - 23:16, 11 May 2025
Finite field (section Polynomial factorization)
"Galois field". In a finite field of order q {\displaystyle q} , the polynomial X q − X {\displaystyle X^{q}-X} has all q {\displaystyle q} elements of...
45 KB (7,535 words) - 18:07, 22 April 2025
uses of normalizing constants include making the value of a Legendre polynomial at 1 and in the orthogonality of orthonormal functions. A similar concept...
6 KB (1,004 words) - 17:38, 19 June 2024
Appell sequence (redirect from Appell polynomial)
mathematics, an Appell sequence, named after Paul Émile Appell, is any polynomial sequence { p n ( x ) } n = 0 , 1 , 2 , … {\displaystyle \{p_{n}(x)\}_{n=0...
7 KB (1,454 words) - 09:14, 10 June 2024