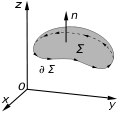
Stokes' theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls, or simply the curl theorem...

the generalized Stokes theorem (sometimes with apostrophe as Stokes' theorem or Stokes's theorem), also called the Stokes–Cartan theorem, is a statement...

special case of Stokes' theorem (surface in R 3 {\displaystyle \mathbb {R} ^{3}} ). In one dimension, it is equivalent to the fundamental theorem of calculus...

a natural, metric-independent generalization of Stokes' theorem, Gauss's theorem, and Green's theorem from vector calculus. If a differential k-form is...

integral theorem and Cauchy's integral formula. The residue theorem should not be confused with special cases of the generalized Stokes' theorem; however...

Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes). The Navier–Stokes equations...

relativity). Kelvin–Stokes theorem Generalized Stokes theorem Differential form Katz, Victor J. (1979). "The history of Stokes's theorem". Mathematics Magazine...

\,\mathbf {q} ]}\nabla \varphi (\mathbf {r} )\cdot d\mathbf {r} .} Stokes' theorem relates the surface integral of the curl of a vector field F over a...

Gabriel Stokes, 1st Baronet, (/stoʊks/; 13 August 1819 – 1 February 1903) was an Irish mathematician and physicist. Born in County Sligo, Ireland, Stokes spent...

Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after L. E. J. (Bertus) Brouwer. It states that for any continuous function f...

vector fields. The corresponding form of the fundamental theorem of calculus is Stokes' theorem, which relates the surface integral of the curl of a vector...

theorem of calculus, the divergence theorem, Green's theorem, and Stokes' theorem as special cases of a single general result, the generalized Stokes...

The fundamental theorem of calculus is a theorem that links the concept of differentiating a function (calculating its slopes, or rate of change at every...

Lord Kelvin to Sir George Stokes containing the first disclosure of the classical Stokes' theorem (i.e., the Kelvin–Stokes theorem). Calculus on Manifolds...

first term, we substitute from the governing equation, and then apply Stokes' theorem, thus: ∮ C D u D t ⋅ d s = ∫ A ∇ × ( − 1 ρ ∇ p + ∇ Φ ) ⋅ n d S = ∫...

and vector calculus, such as the divergence theorem, magnetic flux, and its generalization, Stokes' theorem. Let us notice that we defined the surface...

C {\displaystyle C} , allows us to state the celebrated Stokes' theorem (Stokes–Cartan theorem) for chains in a subset of R m {\displaystyle \mathbb {R}...

calculus, and more generally differential geometry, Stokes' theorem (also called the generalized Stokes' theorem) is a statement about the integration of differential...

and Stokes' theorem simultaneously generalizes the three theorems of vector calculus: the divergence theorem, Green's theorem, and the Kelvin-Stokes theorem...

The proof of Cauchy's integral theorem for higher dimensional spaces relies on the using the generalized Stokes theorem on the quantity G(r, r′) f(r′)...

Stokes shift Stokes stream function Stokes' theorem Stokes wave Campbell–Stokes recorder Navier–Stokes equations Stokes Bay (disambiguation) Stokes Township...

\iint _{S}\left(\nabla \times \mathbf {A} \right)\cdot d\mathbf {S} } (Stokes' theorem) ∮ ∂ S ψ d ℓ   =   − ∬ S ∇ ψ × d S {\displaystyle \oint _{\partial...

Stokes law can refer to: Stokes' law, for friction force Stokes' law (sound attenuation), describing attenuation of sound in Newtonian liquids Stokes'...

form". The forms are exactly equivalent, and related by the Kelvin–Stokes theorem (see the "proof" section below). Forms using SI units, and those using...

Poincaré–Hopf theorem (also known as the Poincaré–Hopf index formula, Poincaré–Hopf index theorem, or Hopf index theorem) is an important theorem that is used...

electromagnetism. It can also be written in an integral form by the Kelvin–Stokes theorem, thereby reproducing Faraday's law: ∮ ∂ Σ E ⋅ d l = − ∫ Σ ∂ B ∂ t ⋅...

2-forms, respectively, and the key theorems of vector calculus are all special cases of the general form of Stokes' theorem. From the point of view of both...

integrating over Ω ( t ) {\displaystyle \Omega (t)} and using generalized Stokes' theorem on the second term, reduces to the three desired terms. Let X {\displaystyle...

{\displaystyle {\boldsymbol {\omega }}=\nabla \times \mathbf {V} .} By Stokes' theorem, the flux of curl or vorticity vectors through a surface S is equal...

instance double integrals, polar coordinates, the Jacobian and the Stokes' theorem) Numerical integration (a technique for approximating a definite integral...