specifically in measure theory, a Borel measure on a topological space is a measure that is defined on all open sets (and thus on all Borel sets). Some authors...

an outer measure μ on n-dimensional Euclidean space Rn is called a Borel regular measure if the following two conditions hold: Every Borel set B ⊆ Rn...

Borel sets of that space. Any measure defined on the Borel sets is called a Borel measure. Borel sets and the associated Borel hierarchy also play a fundamental...

mathematician, he was known for his founding work in the areas of measure theory and probability. Borel was born in Saint-Affrique, Aveyron, the son of a Protestant...

mathematics (specifically in measure theory), a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological...

Lebesgue-measurable sets than there are Borel measurable sets. The Borel measure is translation-invariant, but not complete. The Haar measure can be defined on any locally...

other Borel sets is a Borel probability measure that is neither inner regular nor outer regular. Borel regular measure Radon measure Regularity theorem for...

set that is not contained in the Borel sets. Hence, the Borel measure is not complete. n-dimensional Lebesgue measure is the completion of the n-fold product...

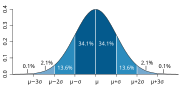
In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space R n {\displaystyle R^{n}} , closely related to the normal distribution...

theory, the Borel–Cantelli lemma is a theorem about sequences of events. In general, it is a result in measure theory. It is named after Émile Borel and Francesco...

Lebesgue–Stieltjes measure, which may be associated to any function of bounded variation on the real line. The Lebesgue–Stieltjes measure is a regular Borel measure, and...

s\in S\}.} Left and right translates map Borel sets onto Borel sets. A measure μ {\displaystyle \mu } on the Borel subsets of G {\displaystyle G} is called...

spectrum) of a measure μ {\displaystyle \mu } on a measurable topological space ( X , Borel ⁡ ( X ) ) {\displaystyle (X,\operatorname {Borel} (X))} is a...

measure spaces, the product space may not be. Consequently, the completion procedure is needed to extend the Borel measure into the Lebesgue measure,...

operators, in which case the PVM is sometimes referred to as the spectral measure. The Borel functional calculus for self-adjoint operators is constructed using...

In compact metric spaces the Borel sets and the Baire sets are the same, so Baire measures are the same as Borel measures that are finite on compact sets...

chemist Borel (crater), a lunar crater, named after Émile Borel Borel algebra, operating on Borel sets, named after Émile Borel, also: Borel measure, the...

have measure zero. Lebesgue measure is an example of a complete measure; in some constructions, it is defined as the completion of a non-complete Borel measure...

support, and the measures can be Baire measures or regular Borel measures or Radon measures or signed measures or complex measures. The statement of...

(a construction known as the Borel hierarchy). There are at least three key motivators for σ-algebras: defining measures, manipulating limits of sets...

centuries that measure theory became a branch of mathematics. The foundations of modern measure theory were laid in the works of Émile Borel, Henri Lebesgue...

{\displaystyle (Y,T)} are Borel spaces, a measurable function f : ( X , Σ ) → ( Y , T ) {\displaystyle f:(X,\Sigma )\to (Y,T)} is also called a Borel function. Continuous...

usual Lebesgue measure cannot be extended to all infinite-dimensional spaces. This is because any translation-invariant Borel measure on an infinite-dimensional...

least as fine as the Borel σ {\displaystyle \sigma } -algebra on X {\displaystyle X} ). A measure/signed measure/complex measure μ {\displaystyle \mu...

principal value Measure (mathematics) Sigma algebra Separable sigma algebra Filtration (abstract algebra) Borel algebra Borel measure Indicator function...

of these measures, and their convolution in particular. Borel measure – Measure defined on all open sets of a topological space Fuzzy measure – theory...

specifically, in geometric measure theory — spherical measure σn is the "natural" Borel measure on the n-sphere Sn. Spherical measure is often normalized so...

true for tempered distributions. The Fourier transform of a finite Borel measure μ on Rn is given by: μ ^ ( ξ ) = ∫ R n e − i 2 π x ⋅ ξ d μ . {\displaystyle...

specifically in measure theory, the Baire sets form a σ-algebra of a topological space that avoids some of the pathological properties of Borel sets. There...

defined using the push-forward and the standard Gaussian measure on the real line: a Borel measure γ on a separable Banach space X is called Gaussian if...