In linear algebra, a circulant matrix is a square matrix in which all rows are composed of the same elements and each row is rotated one element to the...
15 KB (2,841 words) - 10:54, 24 June 2025
n × n Hadamard matrix is that n be a square number. A circulant matrix is manifestly regular, and therefore a circulant Hadamard matrix would have to be...
26 KB (3,716 words) - 16:08, 29 July 2025
cyclic permutation of its vertices. The graph has an adjacency matrix that is a circulant matrix. The n vertices of the graph can be numbered from 0 to n −...
10 KB (1,310 words) - 17:13, 24 May 2025
Grudsky. Circulant matrix, a square Toeplitz matrix with the additional property that a i = a i + n {\displaystyle a_{i}=a_{i+n}} Hankel matrix, an "upside...
15 KB (2,060 words) - 09:17, 25 June 2025
Skew-symmetric matrix (also called antisymmetric or antimetric) Centrosymmetric matrix Circulant matrix Covariance matrix Coxeter matrix GCD matrix Hankel matrix Hilbert...
17 KB (2,812 words) - 21:08, 14 April 2025
Moore–Penrose inverse (redirect from Moore-Penrose Matrix Inverse)
pseudoinverse trivially coincides with the matrix itself: A + = A . {\displaystyle A^{+}=A.} For a circulant matrix C {\displaystyle C} , the singular value...
47 KB (7,644 words) - 13:45, 22 July 2025
Multiplication operator Tridiagonal matrix Toeplitz matrix Toral Lie algebra Circulant matrix Proof: given the elementary matrix e i j {\displaystyle e_{ij}}...
17 KB (2,414 words) - 23:43, 27 June 2025
List of named matrices (redirect from List of matrix)
matrices used in mathematics, science and engineering. A matrix (plural matrices, or less commonly matrixes) is a rectangular array of numbers called entries...
32 KB (1,336 words) - 21:01, 14 April 2025
roots of unity, the companion matrix and its transpose both reduce to Sylvester's cyclic shift matrix, a circulant matrix. Consider a polynomial p ( x...
12 KB (2,500 words) - 21:02, 14 April 2025
DFT matrix becomes a circulant matrix. Multiplying a data sequence with a circulant matrix is equivalent to the cyclic convolution with the matrix's row...
7 KB (1,095 words) - 21:35, 10 December 2024
Paley construction (redirect from Jacobsthal matrix)
are indexed by field elements in the usual 0, 1, 2, … order, Q is a circulant matrix. That is, each row is obtained from the row above by cyclic permutation...
8 KB (1,498 words) - 07:02, 17 June 2025
m ≈ log q {\displaystyle m\approx \log q} . Definition: The nega-circulant matrix of b {\displaystyle b} is defined as: for b = ∑ i = 0 n − 1 b i x i...
16 KB (3,166 words) - 03:27, 7 April 2025
their spatial interactions, then the interaction matrix is circulant. The eigenvalues of a circulant matrix are given by λ k = ∑ j = 0 N − 1 c j γ k j {\displaystyle...
21 KB (3,114 words) - 15:07, 27 August 2024
kernel. Bateman transform Convolution kernel Circular convolution Circulant matrix Differential equations Kernel method List of transforms List of operators...
13 KB (1,278 words) - 15:49, 29 July 2025
consequence of the circular convolution theorem is that the DFT matrix F diagonalizes any circulant matrix. A useful property of the DFT is that the inverse DFT...
76 KB (12,338 words) - 04:38, 31 July 2025
matrix Tridiagonal matrix Block matrix Sparse matrix Hessenberg matrix Hessian matrix Vandermonde matrix Stochastic matrix Toeplitz matrix Circulant matrix...
5 KB (377 words) - 12:12, 30 October 2023
and h are ≤ N, it is reducible to matrix multiplication where the kernel of the integral transform is a circulant matrix. A case of great practical interest...
11 KB (1,276 words) - 12:26, 17 December 2024
lower-cost hardware—in particular, codes constructed such that the H matrix is a circulant matrix. Yet another way of constructing LDPC codes is to use finite...
36 KB (4,626 words) - 16:31, 22 June 2025
fractional integral and fractional derivative. Analog signal processing Circulant matrix Convolution for optical broad-beam responses in scattering media Convolution...
67 KB (8,808 words) - 13:56, 1 August 2025
1&0&1&0&0&-\end{pmatrix}}} Which is circulant, i.e. each row is a cyclic shift of the previous row. Such a matrix is called a C W ( n , k ) {\displaystyle...
16 KB (2,412 words) - 18:58, 2 July 2025
Permanent (mathematics) (redirect from Permanent of a matrix)
determinant of Z. This is a consequence of Z being a circulant matrix and the theorem: If A is a circulant matrix in the class Ω(n,k) then if k > 3, perm(A) > |det...
27 KB (4,567 words) - 03:27, 30 June 2025
Determinant (redirect from Matrix determinant)
square matrix. The determinant of a matrix A is commonly denoted det(A), det A, or |A|. Its value characterizes some properties of the matrix and the...
91 KB (14,413 words) - 00:41, 30 July 2025
Generalizations of Pauli matrices (redirect from Clock and shift matrix)
prime p Hermitian matrix Bloch sphere Discrete Fourier transform Generalized Clifford algebra Weyl–Brauer matrices Circulant matrix Shift operator Quantum...
16 KB (2,766 words) - 13:59, 25 September 2024
convolution or wrapped convolution. It results from multiplication of a skew circulant matrix, generated by vector a, with vector b. Circular convolution theorem...
531 bytes (45 words) - 06:48, 25 November 2022
Commuting matrices (redirect from Matrix commutation)
diagonal matrix commutes with all other diagonal matrices. Circulant matrices commute. They form a commutative ring since the sum of two circulant matrices...
9 KB (1,427 words) - 02:15, 25 May 2025
of order n, the matrix form of an element of K[C] acting on K[C] by multiplication takes a distinctive form known as a circulant matrix, in which each...
10 KB (1,557 words) - 00:17, 16 April 2025
linear complexity test implemented in the TestU01 suite; a Boolean circulant matrix initialized from consecutive bits of an LFSR will never have rank greater...
43 KB (4,864 words) - 20:43, 19 June 2025
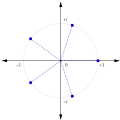
group. The roots of unity appear as entries of the eigenvectors of any circulant matrix; that is, matrices that are invariant under cyclic shifts, a fact that...
41 KB (5,950 words) - 18:05, 8 July 2025
the lepton masses are given by the squares of the eigenvalues of a circulant matrix with real eigenvalues, corresponding to the relation m n = μ [ 1 +...
25 KB (3,712 words) - 10:16, 30 May 2025
analysis: Sparse matrix Band matrix Bidiagonal matrix Tridiagonal matrix Pentadiagonal matrix Skyline matrix Circulant matrix Triangular matrix Diagonally dominant...
70 KB (8,327 words) - 09:12, 7 June 2025