In mathematics, a Fermat number, named after Pierre de Fermat (1607–1665), the first known to have studied them, is a positive integer of the form: F...

Pierre de Fermat (/fɜːrˈmɑː/; French: [pjɛʁ də fɛʁma]; 17 August 1601 – 12 January 1665) was a French mathematician who is given credit for early developments...

In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers a, b...

Fermat number Fermat point Fermat–Weber problem Fermat polygonal number theorem Fermat polynomial Fermat primality test Fermat pseudoprime Fermat quintic...

umask, admirable number 645 = 3 × 5 × 43, sphenic number, octagonal number, Smith number, Fermat pseudoprime to base 2, Harshad number 646 = 2 × 17 × 19...

In additive number theory, the Fermat polygonal number theorem states that every positive integer is a sum of at most n n-gonal numbers. That is, every...

r = 1, it is a Mersenne number. When p = 2, it is a Fermat number. The only known Mersenne–Fermat primes with r > 1 are MF(2, 2), MF(2, 3), MF(2, 4),...

In number theory, Fermat's little theorem states that if p is a prime number, then for any integer a, the number ap − a is an integer multiple of p. In...

Fermat's Last Theorem is a popular science book (1997) by Simon Singh. It tells the story of the search for a proof of Fermat's Last Theorem, first conjectured...

The Fermat prize of mathematical research biennially rewards research works in fields where the contributions of Pierre de Fermat have been decisive:...

The Fermat primality test is a probabilistic test to determine whether a number is a probable prime. Fermat's little theorem states that if p is prime...

decagonal number, centered square number, Fermat pseudoprime 1106 = number of regions into which the plane is divided when drawing 24 ellipses 1107 = number of...

In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem. Fermat's little theorem...

In number theory, Euler's theorem (also known as the Fermat–Euler theorem or Euler's totient theorem) states that, if n and a are coprime positive integers...

makes N a Fermat number. When doing mod N = 2 M + 1 = 2 2 L + 1 {\displaystyle N=2^{M}+1=2^{2^{L}}+1} , we have a Fermat ring. Because some Fermat numbers...

test is a primality test, which can be used to determine whether a Fermat number is prime. It is a variant of Proth's test. The test is named after a...

simple to understand but are very difficult to solve. Examples of this are Fermat's Last Theorem, which was proved 358 years after the original formulation...

73 is also the smallest factor of the first composite generalized Fermat number in decimal: 10 4 + 1 = 10 , 001 = 73 × 137 {\displaystyle 10^{4}+1=10...

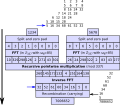
factored the eighth Fermat number using a variant of the Pollard rho algorithm. He later factored the tenth and eleventh Fermat numbers using Lenstra's...

In number theory, a Wieferich prime is a prime number p such that p2 divides 2p − 1 − 1, therefore connecting these primes with Fermat's little theorem...

262,468 = Leyland number 268,705 = Leyland number 271,129 – smallest known Sierpiński prime 274,177 = prime factor of the Fermat number F6 275,807/195,025...

on their limbs. 5 is a Fermat prime, a Mersenne prime exponent, as well as a Fibonacci number. 5 is the first congruent number, as well as the length...

algorithm's most remarkable success was the 1980 factorization of the Fermat number F8 = 1238926361552897 × 93461639715357977769163558199606896584051237541638188580280321...

mathematics, the Fermat curve is the algebraic curve in the complex projective plane defined in homogeneous coordinates (X:Y:Z) by the Fermat equation: X n...

F_{5}} , the first composite Fermat number. 4,294,968,320 = Leyland number using 2 & 32 (232 + 322) 4,295,032,832 = Leyland number using 4 & 16 (416 + 164)...

of two are common in computing. The first 21 of them are: Also see Fermat number, Tetration and Hyperoperation § Lower hyperoperations. All of these...

possible number a 32-bit system can store in memory. Since the prime factors of 232 − 1 are exactly the five known Fermat primes, this number is the largest...

polygon. In number theory, primes of this form are known as Fermat primes, named after the mathematician Pierre de Fermat. The only known prime Fermat numbers...

Manasse, M. S. & Pollard, J. M. (1993), "The Factorization of the Ninth Fermat Number", Mathematics of Computation, 61 (203): 319–349, Bibcode:1993MaCom....

every number of the form 2 n + 1 {\displaystyle 2^{n}+1} with n > 1 {\displaystyle n>1} , including every Fermat number, is a pernicious number. This...