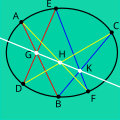
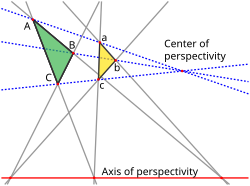
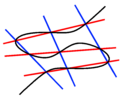
In projective geometry, Pascal's theorem (also known as the hexagrammum mysticum theorem, Latin for mystical hexagram) states that if six arbitrary points...
17 KB (2,198 words) - 00:12, 23 June 2024
entries in Pascal's triangle (Singmaster's conjecture) Pascal matrix Pascal's pyramid Pascal's simplex Proton NMR, one application of Pascal's triangle...
53 KB (7,608 words) - 02:14, 13 June 2025
projective dual of this theorem give Pascal's theorem. As for Pascal's theorem there exist degenerations for Brianchon's theorem, too: Let coincide two...
4 KB (607 words) - 05:18, 22 July 2024
Parabola (redirect from Lambert's Theorem)
{\displaystyle Y_{\infty }} . The 5-, 4- and 3- point degenerations of Pascal's theorem are properties of a conic dealing with at least one tangent. If one...
80 KB (13,447 words) - 19:44, 31 May 2025
Braikenridge–Maclaurin theorem, named for 18th-century British mathematicians William Braikenridge and Colin Maclaurin, is the converse to Pascal's theorem. It states...
2 KB (198 words) - 05:28, 6 April 2024
Pappus's theorem is a special case of Pascal's theorem for a conic—the limiting case when the conic degenerates into 2 straight lines. Pascal's theorem is in...
17 KB (2,865 words) - 22:17, 19 April 2025
sides lie on a line (called the Pascal line). Pascal's work was so precocious that René Descartes was convinced that Pascal's father had written it. When...
63 KB (7,391 words) - 11:21, 11 June 2025
{\displaystyle n} and k {\displaystyle k} can be arranged to form Pascal's triangle. These numbers also occur in combinatorics, where ( n k ) {\displaystyle...
42 KB (6,735 words) - 09:42, 24 June 2025
a projective plane in which the little Desargues theorem is valid for every line. Pascal's theorem Smith (1959, p. 307) Katz (1998, p. 461) (Coxeter...
16 KB (1,788 words) - 02:07, 29 March 2023
suitable ellipse smoothly. The proof of Segre's theorem, shown below, uses the 3-point version of Pascal's theorem and a property of a finite field of odd order...
10 KB (1,934 words) - 02:30, 23 August 2023
20 points associated with a given set of six points on a conic; see Pascal's theorem § Hexagrammum Mysticum Steiner tree problem, an algorithmic problem...
842 bytes (158 words) - 01:33, 30 March 2021
Five points determine a conic (category Theorems in projective geometry)
by applying the Braikenridge–Maclaurin theorem, which is the converse of Pascal's theorem. Pascal's theorem states that given 6 points on a conic (a...
15 KB (2,331 words) - 02:28, 23 September 2023
}}=34650.} One can use the multinomial theorem to generalize Pascal's triangle or Pascal's pyramid to Pascal's simplex. This provides a quick way to generate...
11 KB (2,294 words) - 19:54, 25 June 2025
Brianchon's theorem Ceva's theorem Desargues's theorem Menelaus's theorem Pascal's theorem Poncelet's closure theorem Ptolemy's theorem Apollonian circles...
94 KB (13,156 words) - 20:50, 25 June 2025
Pascal's theorem concerns the collinearity of three points that are constructed from a set of six points on any non-degenerate conic. The theorem also...
69 KB (9,174 words) - 17:05, 5 June 2025
sections drew the attention of 16-year-old Blaise Pascal and helped him formulate Pascal's theorem. The works of Gaspard Monge at the end of 18th and...
38 KB (5,099 words) - 22:20, 24 May 2025
Duality Homogeneous coordinates Pappus's hexagon theorem Incidence Pascal's theorem Affine geometry Affine space Affine transformation Finite geometry...
13 KB (938 words) - 15:07, 19 June 2025
(without seven co-conic ones) are already prescribed. A special case is Pascal's theorem, in which case the two cubics in question are all degenerate: given...
11 KB (1,492 words) - 19:47, 3 May 2025
theorem (geometry) Pascal's theorem (conics) Pasch's theorem (order theory) Pitot theorem (plane geometry) Pivot theorem (circles) Pompeiu's theorem (Euclidean...
78 KB (6,289 words) - 12:34, 6 June 2025
the Conway criterion will tile the plane. Pascal's theorem (also known as the "Hexagrammum Mysticum Theorem") states that if an arbitrary hexagon is inscribed...
31 KB (2,873 words) - 15:07, 3 June 2025
the legs are collinear with the incenter. Pascal's theorem (also known as the Hexagrammum Mysticum Theorem) states that if an arbitrary six points are...
18 KB (2,581 words) - 13:29, 15 May 2025
of a hyperbola is an affine version of the 3-point-degeneration of Pascal's theorem. Area of the grey parallelogram The area of the grey parallelogram...
75 KB (13,585 words) - 01:57, 27 January 2025
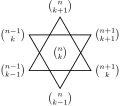
coefficients forming each of the two triangles in the Star of David shape in Pascal's triangle are equal: gcd { ( n − 1 k − 1 ) , ( n k + 1 ) , ( n + 1 k ) }...
4 KB (420 words) - 12:58, 14 May 2025
the angles formed where the extensions of opposite sides intersect. Pascal's theorem states that if six arbitrary points are chosen on a conic section (i...
3 KB (347 words) - 17:21, 26 October 2024
product of projective spaces Rational normal curve Conics, Pascal's theorem, Brianchon's theorem Twisted cubic Elliptic curve, cubic curve Elliptic function...
7 KB (600 words) - 19:55, 10 January 2024
Euclidean geometry (section Pythagorean theorem)
Historically, advanced Euclidean geometry, including theorems like Pascal's theorem and Brianchon's theorem, was integral to drafting practices. However, with...
60 KB (7,199 words) - 23:16, 13 June 2025
Automated theorem proving (also known as ATP or automated deduction) is a subfield of automated reasoning and mathematical logic dealing with proving...
29 KB (2,933 words) - 22:11, 19 June 2025
in the September Number of this Journal "On a new Class of Theorem" and "On Pascal's Theorem"". London, Edinburgh, and Dublin Philosophical Magazine. 37:...
21 KB (2,092 words) - 04:25, 20 May 2025
In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers a, b...
104 KB (11,741 words) - 21:37, 19 June 2025
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle...
94 KB (12,692 words) - 05:47, 14 May 2025