unique Green's function. Green's functions may be categorized, by the type of boundary conditions satisfied, by a Green's function number. Also, Green's functions...
39 KB (5,191 words) - 13:07, 6 May 2025
Green's function number specifies the coordinate system and the type of boundary conditions that a Green's function satisfies. The Green's function number...
15 KB (1,283 words) - 05:03, 14 January 2025
Multiscale Green's function (MSGF) is a generalized and extended version of the classical Green's function (GF) technique for solving mathematical equations...
25 KB (3,525 words) - 00:28, 30 January 2025
kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right),} and the function g(x). (The Green's function number of the fundamental solution is X00.) Therefore, according...
58 KB (9,807 words) - 05:13, 4 May 2025
foresee. True random number generators can be hardware random-number generators (HRNGs), wherein each generation is a function of the current value of...
36 KB (4,422 words) - 19:27, 29 March 2025
the fields of probability, statistics, analytic number theory, and combinatorics. The gamma function can be seen as a solution to the interpolation problem...
90 KB (13,517 words) - 19:06, 28 March 2025
In physics, the Green's function (or fundamental solution) for the Laplacian (or Laplace operator) in three variables is used to describe the response...
11 KB (1,910 words) - 01:17, 15 August 2024
Propagator (redirect from Causal Green's function)
therefore, often called (causal) Green's functions (called "causal" to distinguish it from the elliptic Laplacian Green's function). In non-relativistic quantum...
35 KB (6,183 words) - 18:22, 13 February 2025
the Green's functions used to solve inhomogeneous differential equations, to which they are loosely related. (Specifically, only two-point "Green's functions"...
23 KB (4,547 words) - 03:22, 15 October 2024
then Green's theorem follows immediately for the region D. We can prove (1) easily for regions of type I, and (2) for regions of type II. Green's theorem...
23 KB (4,074 words) - 04:47, 25 April 2025
Busy beaver (redirect from Busy beaver function)
Radó defined two functions related to the busy beaver game: the score function Σ(n) and the shifts function S(n). Both take a number of Turing machine...
66 KB (7,914 words) - 21:22, 30 April 2025
many-body effects, one can resort to so-called Green's function methods. Indeed, knowledge of the Green's function of a system provides both ground (the total...
37 KB (4,835 words) - 08:39, 9 December 2024
diffusion quantum Monte Carlo is a quantum Monte Carlo method that uses a Green's function to calculate low-lying energies of a quantum many-body Hamiltonian...
7 KB (1,171 words) - 01:56, 6 May 2025
Laplace's equation (category Harmonic functions)
the Green's function describes the influence at (x′, y′, z′) of the data f and g. For the case of the interior of a sphere of radius a, the Green's function...
33 KB (5,075 words) - 15:19, 13 April 2025
mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the...
76 KB (11,411 words) - 13:49, 24 April 2025
number), a quadratic function c x 2 {\displaystyle cx^{2}} ( c {\displaystyle c} as a nonnegative real number) and an exponential function c e x {\displaystyle...
35 KB (5,855 words) - 17:54, 17 March 2025
Calculus (redirect from Advanced functions)
output another number. For example, if the doubling function is given the input three, then it outputs six, and if the squaring function is given the input...
75 KB (8,788 words) - 07:15, 30 April 2025
complex distance from the origin. The associated Green's functions are referred as closed-form Green's functions. The method has also been extended for cylindrically-layered...
36 KB (4,006 words) - 09:40, 15 April 2025
converse relation of the function f(w) = wew, where w is any complex number and ew is the exponential function. The function is named after Johann Lambert...
78 KB (12,429 words) - 07:55, 27 March 2025
Helmholtz equation (section Three-dimensional solutions given the function on a 2-dimensional plane)
the eigenvalue, and f is the (eigen)function. When the equation is applied to waves, k is known as the wave number. The Helmholtz equation has a variety...
20 KB (2,976 words) - 04:16, 15 April 2025
a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies...
63 KB (9,504 words) - 08:25, 26 April 2025
linear response functions such as susceptibility, impulse response or impedance; see also transfer function. The concept of a Green's function or fundamental...
6 KB (869 words) - 15:51, 3 February 2025
exponent to which a constant number e ≈ 2.718, the base, is raised. There are several other definitions of the exponential function, which are all equivalent...
37 KB (5,082 words) - 03:28, 5 May 2025
practice, semigroups approximating the delta function arise as fundamental solutions or Green's functions to physically motivated elliptic or parabolic...
96 KB (14,231 words) - 04:12, 23 April 2025
local lattice Green's function, one has to determine the hybridization function such that the corresponding impurity Green's function will coincide with...
19 KB (2,803 words) - 10:18, 6 March 2025
This defines a function R [ X ] → C {\displaystyle \mathbb {R} [X]\to \mathbb {C} } This function is surjective since every complex number can be obtained...
90 KB (11,795 words) - 12:48, 29 April 2025
complicated sums, according to the central limit theorem. Gaussian functions are the Green's function for the (homogeneous and isotropic) diffusion equation (and...
30 KB (5,023 words) - 17:40, 4 April 2025
Taylor series (section Exponential function)
of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the...
48 KB (8,229 words) - 00:43, 11 March 2025
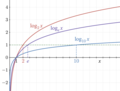
Logarithm (redirect from Logarithmic function)
requires the concept of a function. A function is a rule that, given one number, produces another number. An example is the function producing the x-th power...
98 KB (11,674 words) - 16:13, 4 May 2025
obtain Laplace's equation. Poisson's equation may be solved using a Green's function: φ ( r ) = − ∭ f ( r ′ ) 4 π | r − r ′ | d 3 r ′ , {\displaystyle \varphi...
17 KB (2,371 words) - 13:58, 18 March 2025