number theory, quadratic integers are a generalization of the usual integers to quadratic fields. A complex number is called a quadratic integer if it is a...
22 KB (2,929 words) - 18:53, 28 June 2025
square-free integer different from 0 {\displaystyle 0} and 1 {\displaystyle 1} . If d > 0 {\displaystyle d>0} , the corresponding quadratic field is called...
12 KB (1,306 words) - 02:09, 26 June 2025
quadratic irrational is an irrational root of some quadratic equation with integer coefficients. The quadratic irrational numbers, a subset of the complex numbers...
12 KB (1,691 words) - 02:50, 6 January 2025
Quadratic programming (QP) is the process of solving certain mathematical optimization problems involving quadratic functions. Specifically, one seeks...
22 KB (1,931 words) - 05:55, 18 July 2025
Gaussian integers do not have a total order that respects arithmetic. Gaussian integers are algebraic integers and form the simplest ring of quadratic integers...
35 KB (4,835 words) - 07:01, 5 May 2025
rounding-to-integer functions. The reason this satisfies N(ρ) < N(β), while the analogous procedure fails for most other quadratic integer rings, is as...
14 KB (1,896 words) - 08:34, 5 May 2025
theory, an integer q is a quadratic residue modulo n if it is congruent to a perfect square modulo n; that is, if there exists an integer x such that...
54 KB (5,575 words) - 07:28, 20 July 2025
ideals. The quadratic integer rings are helpful to illustrate Euclidean domains. Quadratic integers are generalizations of the Gaussian integers in which...
126 KB (15,396 words) - 10:40, 9 August 2025
{\frac {1}{2}}(1+{\sqrt {d}}\,)} respectively. See Quadratic integer for more. The ring of integers of the field F = Q [ α ] {\displaystyle F=\mathbb {Q}...
12 KB (1,499 words) - 19:23, 5 June 2025
Hence, any 0–1 integer program (in which all variables have to be either 0 or 1) can be formulated as a quadratically constrained quadratic program. Since...
7 KB (756 words) - 12:35, 5 August 2025
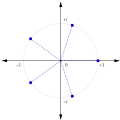
Root of unity (section Relation to quadratic integers)
unity) is a quadratic integer. For n = 5, 10, none of the non-real roots of unity (which satisfy a quartic equation) is a quadratic integer, but the sum...
41 KB (5,950 words) - 18:05, 8 July 2025
in quadratic form. A quadratic form with integer coefficients is called an integral binary quadratic form, often abbreviated to binary quadratic form...
28 KB (4,937 words) - 13:10, 9 August 2025
quadratic form on a vector space. The study of quadratic forms, in particular the question of whether a given integer can be the value of a quadratic...
33 KB (4,600 words) - 17:40, 23 July 2025
decomposition of a positive integer into a product of integers. Every positive integer greater than 1 is either the product of two or more integer factors greater...
25 KB (2,977 words) - 20:54, 9 August 2025
The quadratic sieve algorithm (QS) is an integer factorization algorithm and, in practice, the second-fastest method known (after the general number field...
27 KB (4,572 words) - 05:56, 18 July 2025
Linear programming (redirect from 0-1 integer programming)
case, integer programming problems are in many practical situations (those with bounded variables) NP-hard. 0–1 integer programming or binary integer programming...
61 KB (6,690 words) - 21:36, 9 August 2025
7 (category Integers)
Ramanujan–Nagell equation. 7 is one of seven numbers in the positive definite quadratic integer matrix representative of all odd numbers: {1, 3, 5, 7, 11, 15, 33}...
29 KB (2,747 words) - 19:53, 14 June 2025
real-valued function of an integer or natural number variable). Examples of quadratic growth include: Any quadratic polynomial. Certain integer sequences such as...
4 KB (508 words) - 18:06, 3 May 2025
Modular arithmetic (redirect from Integers mod n)
totient function. Quadratic residue: An integer a is a quadratic residue modulo m, if there exists an integer x such that x2 ≡ a (mod m). Euler's criterion...
29 KB (3,646 words) - 23:20, 20 July 2025
binary quadratic forms is isomorphic to the narrow class group of Q ( d ) {\displaystyle \mathbb {Q} ({\sqrt {d}})} . For real quadratic integer rings...
14 KB (2,326 words) - 00:31, 20 April 2025
Unit (ring theory) (section Integer ring)
constitute the multiplicative group of integers modulo n. In the ring Z[√3] obtained by adjoining the quadratic integer √3 to Z, one has (2 + √3)(2 − √3) =...
11 KB (1,526 words) - 22:40, 5 March 2025
rings of quadratic integers. In summary, if O d {\displaystyle {\mathcal {O}}_{\sqrt {d}}} is the ring of algebraic integers in the quadratic field, then...
36 KB (6,470 words) - 14:24, 29 July 2025
unknown, it is called "univariate". The quadratic equation contains only powers of x that are non-negative integers, and therefore it is a polynomial equation...
53 KB (6,663 words) - 16:21, 26 June 2025
Algebraic number (section Algebraic integers)
algebraic numbers. If the quadratic polynomial is monic (a = 1), the roots are further qualified as quadratic integers. Gaussian integers, complex numbers a...
17 KB (2,302 words) - 10:39, 16 June 2025
{\displaystyle d} is a square-free integer and K = Q ( d ) {\displaystyle K=\mathbb {Q} ({\sqrt {d}}\,)} is the corresponding quadratic field, then O K {\displaystyle...
8 KB (1,132 words) - 21:12, 27 June 2025
martingales Quadratic reciprocity, a theorem from number theory Quadratic residue, an integer that is a square modulo n Quadratic sieve, a modern integer factorization...
3 KB (431 words) - 01:03, 10 August 2025
quadratic reciprocity—Let p and q be distinct odd prime numbers, and define the Legendre symbol as ( q p ) = { 1 if n 2 ≡ q mod p for some integer ...
111 KB (8,574 words) - 22:16, 30 July 2025
Square root (redirect from Square root of integers)
major use in the formula for solutions of a quadratic equation. Quadratic fields and rings of quadratic integers, which are based on square roots, are important...
48 KB (6,213 words) - 04:13, 7 July 2025
Golden ratio (category Quadratic irrational numbers)
of quadratic integers, however the sum of any fifth root of unity and its complex conjugate, z + z ¯ {\displaystyle z+{\bar {z}}} , is a quadratic integer...
115 KB (13,380 words) - 13:49, 22 July 2025
and applied them to quadratic, cubic, and biquadratic reciprocity laws. For an odd prime number p and an integer a, the quadratic Gauss sum g(a; p) is...
9 KB (1,669 words) - 19:06, 30 July 2025